| |||
|
| Home > Astronomy > Site Quality > La Palma Night-Sky Brightness |
La Palma Night-Sky BrightnessChris R. Benn1 & Sara L. Ellison2
1Isaac Newton Group of Telescopes, Apartado 321, E-38700 Santa Cruz de La Palma,
Spain.
Last Updated: 2007 Apr 12. Contents:
Abstract
The brightness of the moonless night sky above La Palma
was measured on 427 CCD images taken with the
Isaac Newton and Jacobus Kapteyn Telescopes on 63 nights during 1987 - 1996.
The median sky brightness, in units of mag arcsec-2,
at high elevation, high galactic latitude
and high ecliptic latitude, at sunspot minimum,
is B = 22.7, V = 21.9, R = 21.0,
similar to that at other dark sites.
The sky brightness
in U and I is less well-determined, U ~ 22.0
(few data),
I ~ 20.0 mag arcsec-2 (variable).
As at other dark sites, the main contributions to sky brightness are
airglow and zodiacal light, in the ratio 2.5:1 at high ecliptic latitude.
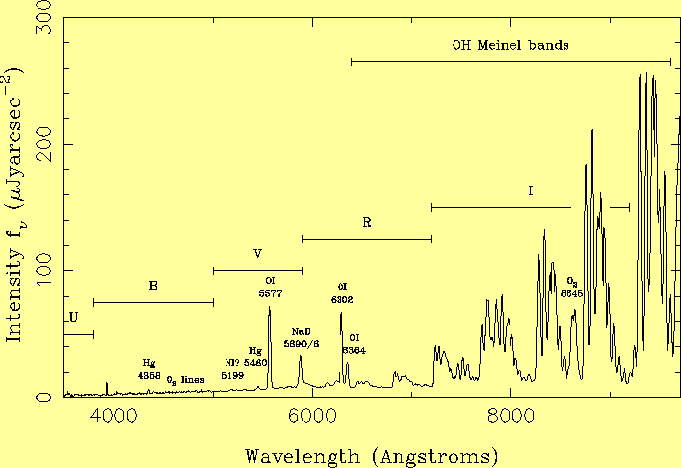
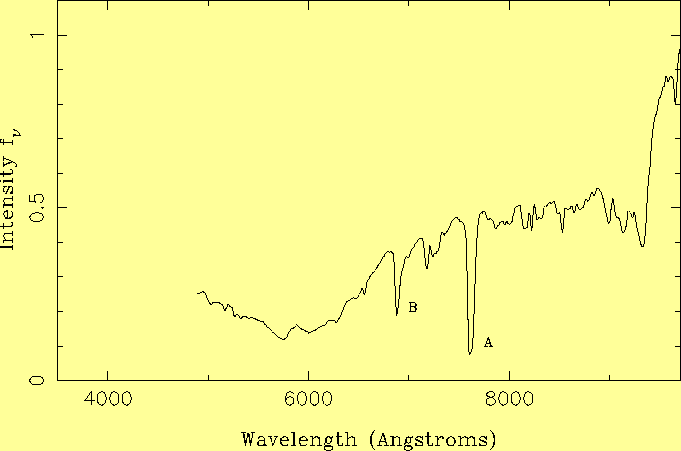
The sky is brighter at low ecliptic latitude (by 0.4 mag); at solar maximum (by 0.4 mag); and at high airmass (0.25 mag brighter at airmass 1.5). The mean brightness of the sky varies by < 0.1 mag with time after astronomical twilight. Light pollution is visible to the naked eye at certain azimuths on the horizon, but its contribution to the continuum brightness at the zenith is < 0.03 mag in all bands, meeting one of the IAU's two recommendations for a dark site. The IAU's second recommendation, that NaD 5890/6-A emission should not exceed in intensity the natural airglow NaD, is not met during the summer, but few spectroscopic observing programmes are likely to be significantly affected. The NaD emission brightens the sky in both V and R broad bands by about 0.07 mag. Total contamination (line + continuum) at the zenith is < 0.03 mag in U, ~ 0.02 mag in B, ~ 0.10 mag in V, ~ 0.10 mag in R. The brightness of the sky shows no dependence on atmospheric extinction Av, for Av < 0.25 mag (as is the case on 80% of nights). The sample includes two nights with Av > 0.25 mag. With Av = 0.4 mag, the sky was brighter by ~ 0.3 mag, and with Av = 0.8 mag by ~ 1.4 mag, probably because of enhanced back-scattering of streetlighting by the dust layer. IntroductionThe zenith brightness of the moonless night sky at a clear dark observing site, measured at high ecliptic and galactic latitudes, and during solar minimum, is typically B = 22.9 mag arcsec-2, V = 21.9 mag arcsec-2, about 10 million times dimmer than the daylight sky (but easily visible to the dark-adapted eye). Some published values are collected in Table 1.The glow of the night sky comprises contributions from a number of sources, summarised in Table 2 (and reviewed by Leinert et al (1998) for 0.1 < lambda < 10 micron). Between the stars, the brightness of the sky is dominated by airglow and zodiacal light, and the night sky is darkest at high ecliptic latitude and low zenith distance, at solar minimum. Typical spectra of the night and twilight skies are reproduced in Figs. 1 and 2.
In the remainder of this section, we introduce the individual contributions to the brightness of the night sky. In Section 2, we report measurements of sky brightness made on La Palma. In Section 3, we compare the median dark-of-moon sky brightness at the observatory on La Palma with measurements made elsewhere; estimate the amount of light pollution; and report how sky brightness varies with time during the night, solar activity, ecliptic latitude, airmass and extinction. Conversion factors between different units commonly used for measuring sky brightness (mag arcsec-2, microJy arcsec-2, Rayleighs A-1, cd m-2, nLamberts) are given in the Appendix.
Sky brightness
Place Nts Year S10.7 U B V R I Reference
MJy mag arcsec^-2
McDonald 5 1960 22.8 21.7 Kalinowski et al (1975)
Junipero Serra 1 1966 23.0 21.9 Walker (1970)
San Pedro Martir 2 1970 1.5 22.9 21.9 Walker (1971)
Junipero Serra 1 1971 1.2 22.9 21.9 Walker (1973)
McDonald 6 1973 1.0 22.7 21.7 Kalinowski et al (1975)
San Benito 1 1976 0.7 22.9 21.9 Walker (1988)
La Silla 1 1978 1.5 22.8 21.7 20.8 19.5 Mattila et al (1996)
Sacramento Peak 12 1978 1.5 21.9 Schneeberger et al (1979)
Kottamia 1 1980 2.0 22.9 21.9 20.1 Nawar et al (1995)
San Benito 7 1981 2.0 22.6 21.6 Walker (1988)
Kitt Peak 7 1987 0.9 22.9 21.9 Pilachowski
et al (1988,9)
Cerro Tololo 2 1987 0.9 22.9 22.0 Geisler (1987)
San Benito 6 1985-7 0.9 22.9 21.9 Walker (1988)
La Palma 4 1987 0.9 21.8 This paper
Cerro Tololo 1 1988 1.6 22.5 21.6 Geisler (1988)
Siding Spring 1989 2.1 22.7 Savage (1989)
Mauna Kea 16 1989-91 2.0 22.7 21.9 Krisciunas (1997)
Calar Alto 3 1990 2.0 22.2 22.6 21.5 20.6 18.7 Leinert et al (1995)
La Palma 9 1990-2 2.0 22.5 21.5 This paper
Cerro Tololo 1 1991 2.0 22.4 Pettini (private comm.)
Mauna Kea 8 1995-6 0.8 22.8 21.9 Krisciunas (1997)
La Palma 43 1994-6 0.8 22.0 22.7 21.9 21.0 20.0 This paper
Table 1 - Near-zenith dark-of-moon broad-band sky brightness measured at various observatories. Nts is the number of nights on which data were taken. S10.7cm is the solar 10.7-cm radio flux density, an indicator of solar activity, measured at Ottawa (Penticton). The last five solar minima occured in 1954.5 (start of cycle 19, largest maximum on record), 1965.0 (cycle 20), 1976.8 (cycle 21), 1986.8 (cycle 22) and 1996.5 (cycle 23). Cycles 21 and 22 were of similar amplitude. As far as can be ascertained from the original references, the quoted solar-minimum sky brightnesses were measured at ecliptic latitude > 40o, ecliptic longitude > 120o from that of the sun, so that variations in the zodiacal-light contribution should affect the total by < 0.1 mag. The San Benito data include faint stars (V > 10). The Mauna Kea data were taken with a photometer with 6.5-arcmin aperure, and may be 0.2 mag too bright due to inclusion in the beam of stars V > 13. The above median values for La Palma (3 ranges of dates) are based on 56 nights of data. The other 7 nights in the sample were not close to either solar minimum or maximum. The table omits any sites where light pollution is believed a priori (e.g. from the models of Garstang 1989a) to raise the sky brightness by >~ 0.1 mag. Calar Alto, Lick, Lowell, Mt Wilson and Palomar are such sites.
Contribution Surface brightness V Typical Vzen
(S10 units) (sunspot min)
Airglow ~ 145 + 130(S_sun - 0.8)/1.2 145
Aurora negligible at |latitude| < 40 deg 0
Zodiacal light ~ 140 - 90 sin(|beta|) (|beta| < 60 deg) 60
~ 60 (|beta| > 60o)
(when > 90o from the sun)
Stars < 55
(V > 20, integ light)
Starlight scattered by ~ 100 exp(-(|b|/10 deg)) 10
interstellar dust
Extragalactic light ~ 1
Light pollution < 20 at a `dark' site (Smith 1979)
----
Total 220
Table 2 - Typical contributions to the V brightness of the moonless night sky. The unit of surface brightness S10 corresponds to one 10th-mag star per square degree (i.e. 27.78 mag arcsec-2); 220 S10 corresponds to V = 21.9 mag arcsec-2, a typical sky brightness at high ecliptic latitudes beta (Table 1) (for beta > 40o the changes are small) during solar minimum, at a site with low geomagnetic latitude. b is galactic latitude. The formula for zodiacal light is an approximate fit to the ground-based results of Levasseur-Regourd & Dumont (1980), for ecliptic longitude > 90o different from that of the sun. The formula for starlight scattered by interstellar dust is an approximate fit to the data presented by Roach & Gordon (1973). Airglow is presumed to contribute the rest of the light, and its variation with solar cycle was deduced from the ~ 0.5 mag brightening at solar maximum (see Section 1.1). Ssun is the solar 10.7-cm radio flux density in MJy; it varies between 0.8 and 2.0 MJy (Section 1.1). The (small) auroral contribution peaks ~ 2 years after the peak of the solar cycle (Roach & Gordon 1973). The zodiacal-light spectrum is approximately solar. That of the airglow is redder than solar for wavelengths > 4500 A, i.e. the fractional contribution of zodiacal light peaks around this wavelength. The integrated light from the airglow over the whole sky corresponds to V ~ -6 (cf Venus -4, full moon -13). 1.1 AirglowThe airglow is emitted by atoms and molecules in the upper atmosphere which are excited by solar UV radiation during the day (Ingham 1972). Airglow is the brightest component of the light of the night sky and it contributes the main spectral features to the night-sky spectrum (Fig. 1), including the 5577- and 6300-A lines from OI (both also prominent in the spectrum of the aurora), the ubiquitous 5890/6-A NaD doublet (the Na may be from sea salt carried to high altitude) and the bright OH rotation/vibration (Meinel) bands in the red and IR. The atoms and molecules responsible for individual features lie in well-defined layers of the atmosphere e.g. the O2 Herzberg bands, OI 5577 A, NaD 5890/6 A and the OH bands arise at an altitude of 90 - 100 km (mesopause, D layer) while OI 6300, 6364 A and O2 8645 A arise at ~ 300 km (F2 layer of ionosphere). The airglow lines are ~ 1000 times brighter during the day. The brightness of the airglow correlates with solar activity, e.g. with the 10.7-cm radio flux density S10.7cm, which in turn correlates with the intensity of solar EUV radiation (100 - 600 A) striking the upper atmosphere (Chatterjee & Das 1995). S10.7cm varies approximately sinusoidally during the solar cycle, from ~ 0.8 MJy at solar minimum, to ~ 2.0 MJy at solar maximum (typical values; the amplitude of the solar cycle, and presumably the effect on sky brightness, varies). The sky is ~ 0.5 mag brighter at solar maximum, judging from monitoring carried out at three sites: Hawaii 1985-96 (Krisciunas 1990, 1996, 1997); San Benito 1976-87 (Walker 1988); and La Silla 1989-93 (Leinert et al 1995). The La Silla data are omitted from Table 1; they were taken through a narrow-band filter. Some dimming of the airglow might be expected after astronomical twilight, which is approximately the time at which sunset is seen from an altitude of 100 km. The 6300-A OI emission line decays rapidly after twilight, the 5577-A line does not. Walker (1988) reported that the B and V sky brightness at San Benito decreased by 0.4 mag during the first half of the night, with no change after midnight. Krisciunas (1990, 1997) found evidence for a small decrease during the night in the brightness of the sky over Hawaii, but using few data. Pilachowski et al (1989), Leinert et al (1995) and Mattila et al (1996) detected no systematic variations with time during the night at Kitt Peak, Calar Alto and La Silla respectively. The brightness of the airglow can vary randomly, by up to a few 10s of %, with position on the sky and with time during the night (Shefov 1972, Roach & Gordon 1973, Turnrose 1974, Kalinowski et al 1975, Pilachowski et al 1989, Krisciunas 1997, Leinert et al 1998). Some of the variations at different wavelengths are correlated (Chamberlain 1961, Leinert et al 1995), e.g. the strength of the 5577-A line correlates with that of the green/blue pseudo-continuum. The variations in intensity of the 5577-A emission with time and position are suggestive of clouds of emitting material drifting across the line of sight at air speeds typical of the 100-km altitude. The brightness of the OH Meinel bands in the red and infrared can vary by a factor of 2 during the night, and during the year, and can show quasi-periodic variations with time (probably atmospheric oscillations, Leinert et al 1998). The strength of at least the NaD line varies with season; ~ 30 Rayleighs in local summer vs ~ 180 Rayleighs in winter (Allen 1973). Other complex variations with time are known. For example in winter the 6300-A line can brighten abruptly sometime before midnight, when the ionosphere at the `conjugate point' on the other side of the globe sees sunrise, releasing a flood of charged particles along the earth's magnetic-field lines (Ingham 1972). The airglow is about twice as bright at geomagnetic latitude 70o as at latitude 20o (Allen 1973). The intensity of the 6300-A line shows a complex dependence on geomagnetic coordinates. Roach & Gordon (1973) give a map based on measurements from a few satellite passes; the strengths in Rayleighs above different observatory locations were: La Palma 100 (the strength of the line in Fig. 1 is about 160 Rayleighs); Hawaii 400; Chile < 50; and Siding Spring < 50. Variations in the brightness of the airglow triggered by lunar and solar tides in the atmosphere have been reported, but a recent study at La Silla found none (Mattila et al 1996 and references therein). 1.2 Zodiacal lightZodiacal light is sunlight scattered by interplanetary dust. It contributes up to half the brightness of the night sky. Its intensity as a function of ecliptic latitude beta and helioecliptic longitude lambda - lambdasun was tabulated by Levasseur-Regourd & Dumont (1980) (earlier tabulations e.g. by Roach & Gordon 1973, overestimate the brightness by factors up to ~ 2). The Levasseur-Regourd & Dumont results agree with those obtained from space (Helios A and B) to within ~ 10% (Leinert et al 1998). For ecliptic longitude more than 90o from that of the sun, the intensity varies by a mean factor ~ 2.3 between ecliptic pole beta = 90o and plane beta = 0o (see Table 2). Along the plane beta = 0, the intensity is minimum at helioecliptic longitude lambda - lambdasun ~ 140o, rising to 3 times the polar brightness in the anti-sun direction lambda - lambdasun = 180o. This weak glow in the anti-sun direction, the gegenschein, is just visible to the naked eye under good conditions, over a patch ~ 20o x 10o along the ecliptic, with excess brightness ~ 40 S10 units (James et al 1977). It is thought to be due to the same mechanism that causes the surge in the brightness of the moon when nearly full: the invisibility of shadowed regions on the observed object when sun, observer and object are in line. The brightness on the ecliptic may also increase slightly 60o either side of the moon, due to scattering from dust accumulated at the earth-moon L4, L5 Lagrangian points (Kordylewski 1961, Mercer et al 1978). The intensity of the zodiacal light varies little with solar cycle because the luminosity of the sun in the visible waveband varies by < 1% (Lockwood et al 1980). There are time variations of a few % at high ecliptic latitudes due to a slight inclination of the dust-cloud's plane of symmetry with respect to the ecliptic (James et al 1997), and due to the eccentricity of the earth's orbit (Dumont & Levasseur-Regourd 1972). Zodiacal light dims as R-2.3 with increasing distance R of the observer from the sun, for 0.3 < R < 3 astronomical units (Leinert et al 1977), and is negligible when the sky is viewed from beyond the solar system's asteroid belt (Toller et al 1987).The spectrum of zodiacial light is very similar to that of the sun over the UV - IR range (Weinberg & Sparrow 1978), and its fractional contribution to the brightness of the night sky peaks at a wavelength of 4500 A (O'Connell 1987) (~ 0.5 of total for ecliptic latitude beta = 30o). By 8000 A, the brightness of the OH airglow bands has reduced the zodiacal light's fractional contribution to ~ 0.1. In the UV, the fractional contribution falls off dramatically with decreasing wavelength, and shortward of 2500 A, the non-airglow contribution is dominated by starlight scattered by interstellar dust. From space, the sky at 2000 and 10000 A is a factor ~ 40 fainter than from the ground, compared with a factor ~ 2 in the optical (O'Connell 1987). It is important to take the contribution of zodiacal light into account when studying diurnal or seasonal variations of zenith sky brightness. For example, at typical geographical observing latitudes 20 - 40o, the midnight sky brightness at the zenith is lowest during local summer (ecliptic low), highest during local winter (ecliptic high), mimicking a seasonal variation. 1.3 StarlightStarlight contributes substantially to the integrated brightness of the sky; in S10 units:(approximate fit to the data of Roach & Gordon 1973, b = galactic latitude). If all the starlight were scattered uniformly over the sky, it would produce a background of ~ 100 S10 units. However, most of this light is from stars with 6 < V < 16 and published measurements of sky brightness usually now refer to the sky between the stars. Stars fainter than V = 20 (easily detected in a 10-minute CCD exposure with a 1-m telescope) contribute insignificantly to the total brightness of the night sky. Starlight scattered by interstellar dust produces a diffuse glow concentrated along the galactic plane, analagous to the zodiacal light along the ecliptic (see Table 2). As noted above, for wavelengths shorter than 2000 A, this dominates the brightness of the sky as seen from outside the earth's atmosphere (Paresce & Jakobsen 1980). 1.4 Extragalactic lightThe extragalactic contribution to the brightness of the night sky is very small (Wesson 1991 explains why). Spinrad and Stone (1978) set a conservative upper limit < 5 S10, and measurements from the Pioneer spacecraft, when > 3 A.U. from the sun, set an upper limit < 4 S10 (Toller et al 1987). A lower limit can be estimated from the faint galaxy counts, B < 28, given e.g. by Longair (1993, fig. 17) and Hogg et al (1997). The contribution of these to the brightness of the night sky peaks at about 0.06 S10 mag-1 for B = 25, with total 0.4 S10 for 20 < B < 28, corresponding to ~ 1.0 S10 in V band if B-V ~ 1. Leinert et al (1998) give a summary of recent upper (photometry) and lower (galaxy-counts) limits on the intensity of the extragalactic background light.Although extragalactic light contributes only ~ 1% of the total sky brightness, its distribution on the sky is uneven (see e.g. Cole, Treyer & Silk 1992) and it may have a disproportionate effect on the signal-to-noise of observations of faint objects (e.g. Davies et al 1994). When photon noise from a smooth sky background is the limiting factor, signal-to-noise rises with integration time tau as tau0.5. However, a discrete object within the photometry aperture will produce an error in the measurement of intensity which is independent of tau. Since apertures are typically a few arcsec in diameter (to be > seeing), the effect becomes important for objects with a density on the sky ~ (few arcsec)-2, i.e. V > 21. At this level, and fainter, the object counts are dominated by galaxies rather than stars. E.g. the galaxy counts from Longair (1993) indicate that there is a probability ~ 20% of including a galaxy with B < 24 within a randomly-positioned aperture of size 5 x 5 arcsec2. This will cause an error in the measured flux of a B = 23 target object of 40%, much greater than that due to airglow/zodiacal-light photon noise during a short dark-of-moon exposure with a 1-m telescope. 1.5 Light pollutionLight pollution at observatory sites (McNally 1994, Holmes 1997) arises principally from tropospheric scattering of light emitted by sodium- and mercury-vapour and incandescent street lamps. Lighting wastefully emitted above the horizontal costs the US taxpayer ~ 109 $ year-1, more than the cost of funding US astronomy (Hunter & Crawford 1991).Typical street-lamp spectra were presented by Osterbrock et al (1976). The 4358-A Hg line can be a hazard for observers wanting to compare the intensities of the 4363 and 5007-A OIII lines (for measuring the temperature of astrophysical plasmas). The 5460-A Hg line lies in the centre of the y band of the ubvy system. The NaD 5890/6-A line typically contaminates both the V and R passbands. Models of the contribution of city lighting to dark-sky brightness were presented by Treanor (1973), Walker (1973), Yocke et al (1986) and Garstang (1984, 1986, 1989, 1991a,b,c). Walker (1977, 1991) and Garstang (1989) estimate the increase in brightness at zenith distance 45o, in the direction of a conurbation of population P at distance D km to be ~ PD-2.5/70 mag. The sky near the horizon is brightened in directions both towards and away from a source of light pollution (Berry 1976). The IAU recommendations for a dark site are continuum Delta mag < 0.1 for 3000 < lambda < 10000 A, and intensity of NaD light pollution < that from airglow, at ZD = 45o towards any city (Smith 1979, appendix 4.1 of McNally 1994). 1.6 MoonlightMoonlight brightens the sky by about 1 mag (quarter moon, phase 0.5) to 4 mag (full moon) in U, B and V. The brightening is less dramatic in the red, ~ 2 mag in I at full moon. The moonlit sky brightness depends strongly on a number of parameters. A model of sky brightness as a function of lunar phase, lunar zenith distance, distance from the moon etc. was presented by Krisciunas & Schaefer (1991). In this paper, we consider only the brightness of the moonless sky.1.7 The effect of airmassAt high airmass, light from outside the atmosphere may be dimmed by scattering and absorption, but the airglow will probably be brighter, since a line of sight intercepts a larger number of atoms in the airglow layer. For airglow arising in a thin layer at height h, the intensity should vary with zenith distance ZD aswhere a is the radius of the earth (van Rhijn 1921). (The dependence on zenith distance of the intensity of a given emission line can be used to determine the height of the airglow species responsible.) For XD < 70 deg, I(ZD) ~ airmass ~ sec(ZD). If a fraction f of the sky brightness is due to airglow, one expects the sky to be Mattila et al (1996) observed the 1978 La Silla sky brightness to be about 0.05 mag brighter at ZD = 30o than at the zenith, while Leinert et al (1995) reported that at Calar Alto in 1990, the sky was 0.1 mag brighter at ZD = 40o. These two measurements are broadly consistent with the prediction of the second equation above. 1.8 The effect of dustDust suspended in the atmosphere absorbs and scatters incoming light. The darker parts of the sky can thus be brightened by scattered zodiacal light (from the ecliptic) and starlight (from the Milky Way) by up to a few 10s of % (Leinert et al 1998), or by moonlight (several magnitudes, as mentioned above). More importantly, dust backscatters streetlighting, the spacebound flux from which may be comparable in intensity with inbound extraterrestrial light and airglow, ~ 10 Wkm-2 over the visible range (see Section 3.6 and Table 5). Garstang (1988, 1991a,b) presented models of the effect of dust on light pollution.2.0 Measurements from La PalmaLa Palma in the Canary Islands hosts Europe's largest Northern-hemisphere observatory, the Observatorio del Roque de los Muchachos (Murdin 1985). The observatory lies close to the island's peak, on the rim of a large volcanic caldera, at longitude 18o W, latitude 29o N, altitude 2300 m, geomagnetic latitude ~ 20o N. Approximately 70% of the nights are clear (95% in the summer) and 60% are photometric. The median site seeing is ~ 0.7 arcsec (Munoz-Tunon et al 1997). Atmospheric extinction is typically 0.15 mag in V, but can be substantially higher during the summer (Figs. 3,4), when dust from the Sahara desert (400 km away) blows over the Canary Islands. The island has a population of ~ 80000 people, but light-pollution is strictly controlled.
Dark-of-moon sky brightness was measured from images in the electronic data archive of the Isaac Newton Group of telescopes. This archive includes all digital (mainly CCD) data taken with the 4.2-m William Herschel, 2.5-m Isaac Newton and 1.0-m Jacobus Kapteyn Telescopes. It currently (1997) comprises ~ 430000 CCD exposures, ~ 50% of which are direct images. Most of the direct images are taken through broad-band U, B, V, R or I filters (very few in Z) with the 2.5-m or 1.0-m telescopes. The 4.2-m telescope is used mainly for spectroscopic work. For this study, only images taken with the moon below the horizon and during astronomical night (sun at least 18o below the horizon) were used. We concentrated on nights when several observations had also been made of photometric standard stars, and avoided periods when poor observing conditions were logged. Nights on which the Carlsberg Automatic Meridian Circle did not record a measure of extinction (usually because the night was not photometric) were excluded. Most of the data are drawn from the solar-minimum years 1994-6, but we also sampled the other years (> 1987) covered by the archive. In all, we measured the background brightness on 397 images taken on 58 nights with the Isaac Newton Telescope and 30 images on 5 nights with the Jacobus Kapteyn Telescope.
Sky brightness was measured in areas
apparently free of nebulosity, stars, cosmic-ray events or CCD defects.
Photometric calibration was obtained from the archived observations of
standard stars (usually from the list of Landolt 1992)
on the same night.
Sky brightness was calculated for each band, as follows:
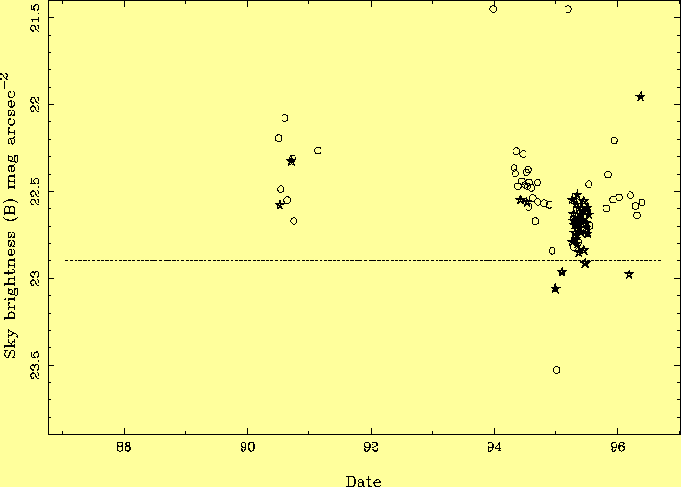
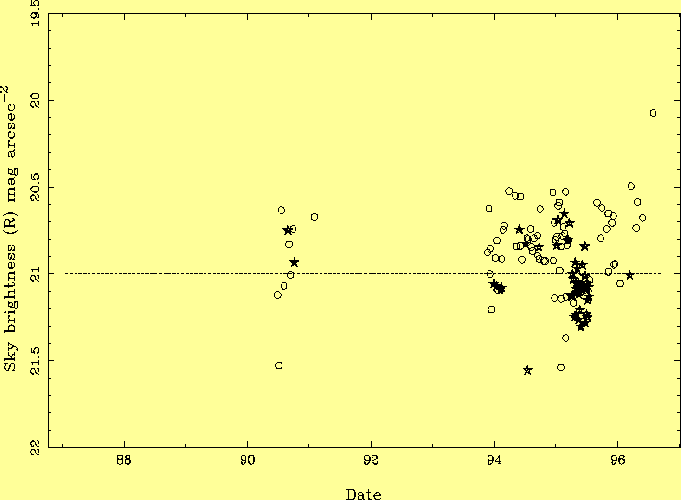
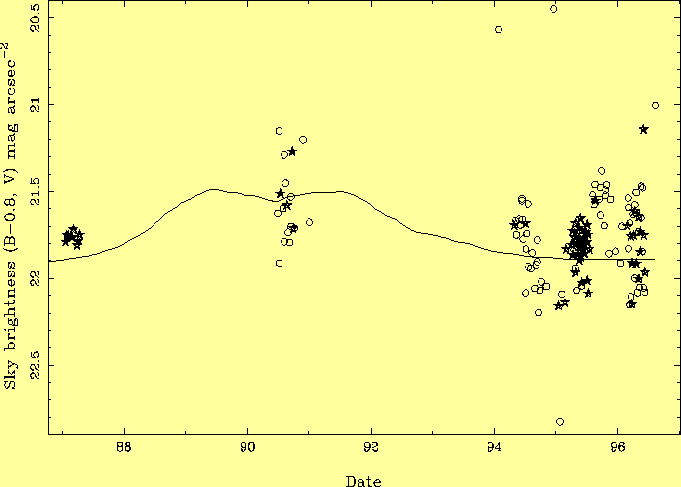
Zeropoint (apparent mag for 1 count/sec): Counts sec-1 pixel-1 from sky: Sky brightness in mag arcsec-2: where sky is the sky-background level on the exposures of standards; bias is the CCD bias level; counts and bias are within an aperture for the standard, and per pixel for sky; tauST and tauSK are the exposure times on standards (typically a few seconds) and sky (typically 200 - 1000 seconds); mapp is the catalogue apparent magnitude of the standard star in the relevant band; ext is the atmospheric extinction in magnitudes for the standard star (airmass x zenith extinction); and scale is the angular scale at the CCD (between 0.3 and 0.6 arcsec/pixel). In the equation for ZST, the mean zeropoint ZST for the given band for the night was used. Note that the standard-star magnitudes have been corrected for extinction, the sky brightnesses have not, following the convention adopted in most of the recent studies of sky brightness (e.g. by Walker 1988, Krisciunas 1990, Lockwood et al 1990, Leinert et al 1995, and Mattila et al 1996). Correcting the sky brightness for extinction would be appropriate only if the extinguishing layer were known to be below all sources of sky brightness, which is not the case; and would be feasible only if the relative amounts of extinction due to absorption (affecting light from stars and sky) and scattering (affecting only light from stars) were known. To minimise the amount of data-reduction required, the CCD images were not flat-fielded. On the EEV and TEK CCDs in use during this period, the rms sensitivity variations are about 5% pixel to pixel and over larger areas. Since the sky brightness measurements were averaged over many pixels, and the counts from the standard stars were typically spread over ~ 10 pixels, omission of flat-fielding introduces errors <~ 5% into the measurements of sky brightness. To exclude non-photometric nights, data were discarded if the rms on the zeropoints for the standard stars was > 0.2 mag in any band, or, in a few cases, if the measured zeropoint was grossly different from that obtained with the same instrument/detector combination on other nights. The zeropoint for a given CCD is stable to < 10% from night to night. The analyses reported in the following sections are based on 427 sky-brightness measurements and 451 observations of standard stars, made during 63 nights at the Isaac Newton and Jacobus Kapteyn Telescopes. 3.0 ResultsAs noted in the introduction, sky brightness depends significantly on a number of parameters, and these dependencies may differ from site to site. The large size of the dataset described in Section 2 helps in disentangling these dependencies for La Palma, and also in averaging out the effects of short-term variations in airglow noted in previous studies. In each of the analyses below, all but one of the following criteria (depending on the parameter being investigated) have been used in isolating a small subset of clean data (plotted in each accompanying figure) from the full set: date of observation later than 1994.0 (for solar minimum); ecliptic latitude > 40o or > 30o; galactic latitude > 10 deg; zenith extinction for night < 0.2 mag; airmass < 1.4. This selection limits to < 0.1 mag the effect on sky brightness of the variation of any individual parameter. Quoted values of sky brightness are medians rather than means, and quoted errors on the median are dx/sqrt(N) where +- dx includes 2/3 of the points, and N is the number of points.3.1 Mean sky brightness and variation with solar cycleLa Palma sky brightness is plotted against date in Figs. 5 - 8. The median values (of the high-ecliptic-latitude data represented by stars) during solar minimum 1994-6 are B = 22.7 +- 0.03, V = 21.9 +- 0.03, R = 21.0 +- 0.03 mag arcsec-2, with a scatter of about 0.15 mag in each band. A few measurements in V are also available from 1987 (previous sunspot minimum) with median V = 21.8 mag arcsec-2. The brightnesses in V and R are similar to those measured at the other sites listed in Table 1 (mostly in the Americas). The measured brightness in B is 0.2 mag higher than the pre-1990 data in Table 1, but the median is dominated by 1995 data, and is consistent with a trend found by Krisciunas (1997) from 14 measurements at Mauna Kea during 1993-6, showing a steady decline from 22.3 to 22.9 mag arcsec-2 over this period, i.e. the B sky brightness was not at a minimum in 1995 even though the 10.7-cm radio intensity of the sun was at a minimum throughout 1994-6. (The relatively brighter sky in B is unlikely to be due to light pollution, which affects mainly the V and R bands.) The 0.15-mag scatter in the measured values is a combination of measurement errors (inaccurate extinction values, lack of flat-fielding) and true variations in sky brightness.
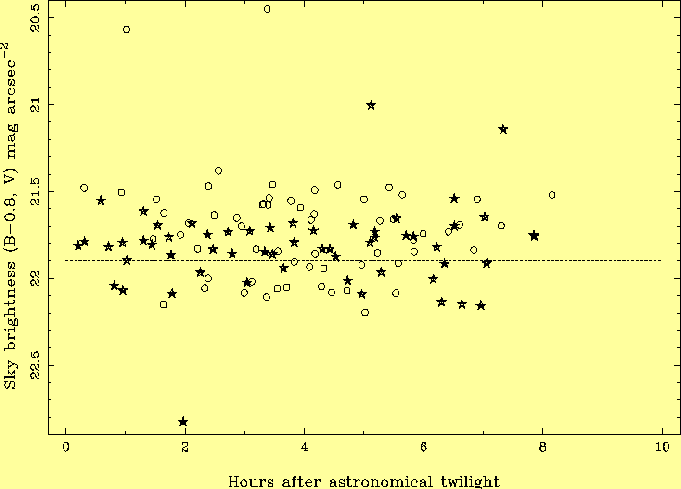
Although these data sample only sparsely the period of solar maximum ~ 1990, an enhancement of sky brightness at that time is evident in Fig. 8, which includes both the B and V data, corrected for the contribution from zodiacal light. The sky was 0.4 +- 0.1 mag brighter in 1990 than in 1995. In R, the large variations in airglow intensity mask any changes with solar cycle, but assuming that the relative contributions of airglow and zodiacal light in V given in Table 2, that the brightness of the R airglow is proportional to that in V, and that the zodiacal light has the spectrum of a 6000-K blackbody, the predicted variation in total R sky brightness with solar cycle is ~ 0.5 mag. No measurements were made close to the time of the Pinatubo (1993.5) volcanic eruption, but the sky probably brightened then by a few tenths of a mag (Krisciunas 1996). There are fewer measurements in U and I bands; the median sky brightnesses are U ~ 22.0, I ~ 20.0 mag arcsec-2, broadly consistent with the few values measured elsewhere (Table 1). The I brightness is dominated by OH (Meinel) emission bands (Fig. 1) and varies by up to a factor ~ 2 during the night. 3.2 Variation with time during the nightLa Palma sky brightness is plotted against time after astronomical twilight in Fig. 9.
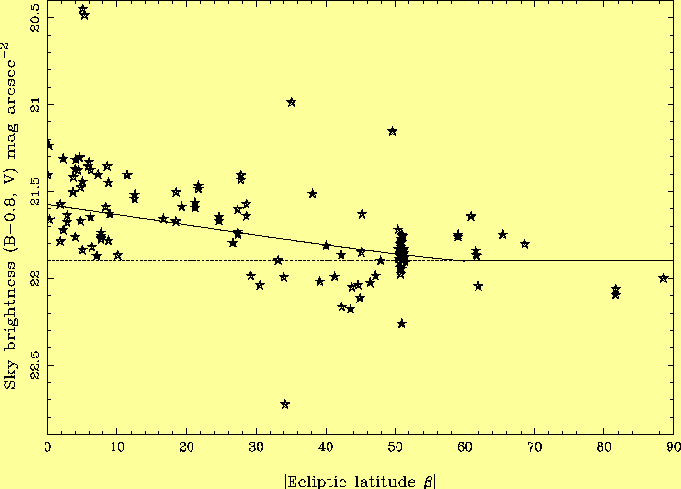
The difference between the sky brightnesses at the beginning and end of the night is 0.03 +- 0.07 mag, consistent with zero. A similar plot against hours before dawn astronomical twilight provides no support for the idea that the sky is darkest before dawn. These results contrast with the finding by Walker (1988) that the sky brightness at San Benito dimmed by ~ 0.4 mag in B and V during the first half of the night. However, some of the variation he saw might be due to the diminishing contribution of zodiacal light at the zenith. This effect is particularly pronounced in the spring, when Walker observed, because at zenith both ecliptic latitude and helioecliptic longitude increase after astronomical twilight, and the zenith brightness will diminish by ~ 0.25 mag during the first half of the night (assuming the zodiacal-light distribution measured by Levasseur-Regourd & Dumont 1980). Walker noted this possibility but thought the intensity of the zodiacal-light varaiations too small to account for the effect he observed. After astronomical twilight, the prominent 6300-A line diminishes rapidly in intensity, e.g. on 24 June 1995 from 150 A to 30 A equivalent width. This implies a small (<~ 0.1 mag) diminution in the broad-band R sky brightness. No variation > 0.1 mag is visible in a plot of R sky brightness against time after twilight. 3.3 Variation with ecliptic coordinatesLa Palma sky brightness is plotted against ecliptic latitude beta in Fig. 10. The variation observed (0.4 mag brighter on the ecliptic than at the poles) is consistent with that predicted by the formula given in Table 2 (solid curve).
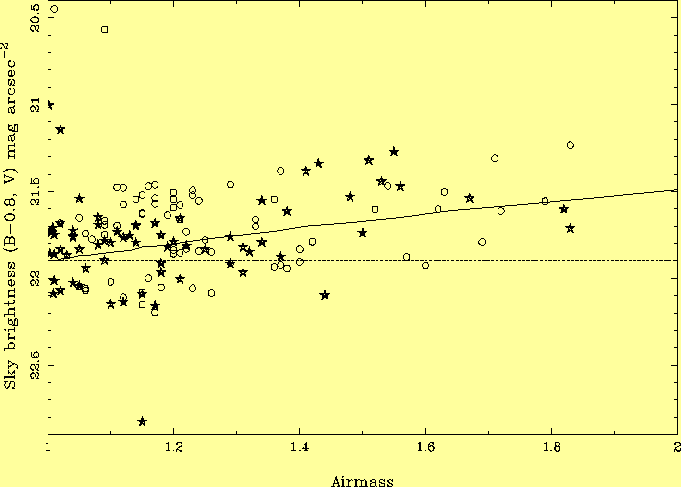
10 measurements were made at |beta| < 5 deg. One of these lies in the expected region of the gegenschein between 170 and 190o in longitude from the sun. It is 0.3 mag brighter than the median of the other 9, consistent within the errors with the 0.2 mag brightening expected in the antisun direction (Section 1.2). 3.4 Variation with galactic latitudeFew (< 2%) of the archive images examined were taken at galactic latitude b < 30o, For b > 30o, there is no significant variation (< 0.1 mag) with b, consistent with the ~ 0.05 mag variation expected from the formula given in Table 2 for starlight scattered by interstellar dust.3.5 Variation with airmassLa Palma sky brightness is plotted against airmass in Fig. 11. The sky is 0.25 +- 0.07 mag brighter at airmass ~ 1.5 than it is at the zenith. The second equation in Section 1.7 can be used to deduce from this the fraction of the sky brightness due to airglow, f = 0.6 +- 0.15, consistent with that assumed in Table 2 (f = 0.7 at solar minimum).
3.6 Light pollution80000 people live on La Palma, mostly in or near nine small towns lying between 10 and 15 km from the observatory (Rodriguez et al 1990). Other possible sources of light pollution include the neighbouring islands of La Gomera, El Hierro and Tenerife (which has floodlit tourist beaches). There is a direct line of sight from the observatory to sea level on all three islands (line-of-sight range to sea level ~ 120 sqrt(A) km, where A is the altitude of the observer in km). Clouds lying below the observatory often blot out streetlighting, although during the summer months they tend to be dispersed by warm winds. Azimuths (north through east), populations and distances of potential light-polluting communities are summarised in Table 3. There are no important sources of light pollution north and west of the observatory. The last column of Table 3 gives Delta magG, the increases in sky brightness predicted by the models of Garstang (1989) for the given populations and distances. These are based on an average 1000 lumens illumination person-1. The actual value for La Palma is ~ 1500 lumens person-1, but much less of the latter escapes into the sky than for a typical US city; the calculated Delta magG serve mainly to indicate approximate relative amounts of light pollution expected in different directions.
Place Azimuth Population Distance Delta mag_G
(deg) (1986) km
Barlovento 50 3000 10 0.06
Los Sauces / San Andres 110 6000 12 0.08
Tenerife 115 600000 130 0.02
Santa Cruz 125 18000 15 0.18
Brena Alta/Baja 140 8000 15 0.08
La Gomera 140 17000 90 <0.01
El Paso 180 7000 12 0.10
El Hierro 190 7000 110 <0.01
Los Llanos / Tazacorte 200 23000 12 0.32
Table 3 -
Possible
sources of light pollution at the observatory on La Palma.
The estimated changes in zenith sky brightness given in the last column
are from the model of Garstang (1989a).
They are likely to be overestimates (see text) but give a rough idea of the
relative contributions to be expected from different sources.
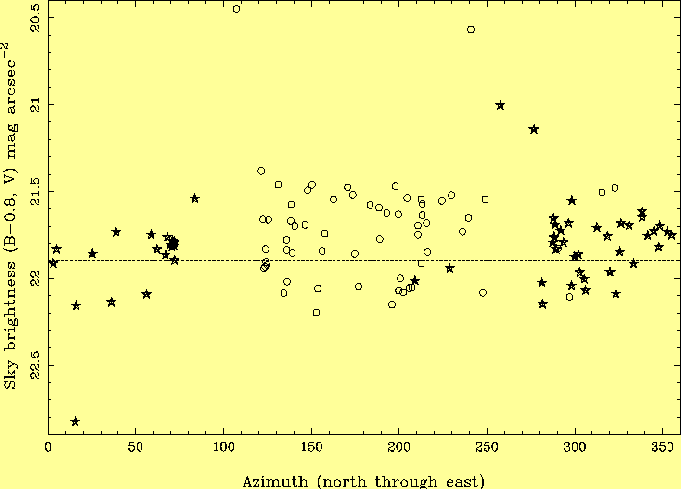
Orange glows are visible to the naked eye at azimuths ~ 50, 120, 190. The most luminous contributor is the island of Tenerife, but visual inspection of the horizon confirms what Table 3 suggests, that the glow in this direction is not particularly bright, and that lighting on Tenerife does not threaten the quality of the La Palma sky. Most of the contaminating light is from La Palma's 14000 streetlamps, which consume ~ 2 MW of electrical power and emit ~ 120 Mlumens, ~ 180 kW, of visible light (see Appendix for conversion factors). Approximately half of the light generated emerges from the lamp housing, and ~ 10% of the emerging light is reflected from the ground, so ~ 9 kW, or ~ 10 Wkm-2 (island area = 700 km2) escapes to the sky. This is comparable with the inbound light of the night sky, ~ 10 W km-2 (see Table 5), so that significant back-scattering by the atmosphere constitutes a light-pollution hazard. The fractional illumination provided by each type of lamp is given in Table 4.
Contamination of sky brightness (mag)
Type of lamp Philips Flux U B V R
brand %
Sodium low-pressure SOX 49 0 0 0.05 0.04
Sodium high-pressure SON-T 21 0 <0.01 0.03 0.02
Mercury HPL-N 13 <0.03 0.02 0.01 0.02
Incandescent 15 <0.01 <0.01 0.01 0.02
Total <0.03 0.02 0.10 0.10
Table 4 -
Contamination of the sky above the observatory by streetlamps
on La Palma. The first 3 columns give the lamp type,
commonest Philips' serial
and fraction of total lumens illumination on La Palma
(information supplied by Javier Diaz of the Oficina Tecnica para la
Proteccion
de la Calidad del Cielo).
Fluorescent lamps contribute a negligible fraction of the total
illumination, ~ 2%.
Columns 4 - 7 give the brightening of the
sky above the observatory in mag for line
plus continuum emission from the
lamps, as estimated in Section 3.6
(U = 3200 - 3800 A, B = 3800 - 5000 A, V = 5000 - 5900 A,
R = 5900 - 7200 A).
The effect of NaD emission on the brightness of the sky in V and R is
less than it otherwise might be because the line enters
near the edge of the passbands in both cases (typically ~ 0.6 x
maximum in V, ~ 0.75 * maximum in R for the passbands
used for the observations described in this paper).
A royal decree of 1992 (La Ley del Cielo, reproduced in appendix 6 of McNally 1994) strictly limits outdoor night-time illumination on La Palma. Low-pressure sodium lamps must be used except in urban areas; the fraction of ultraviolet light emitted by lamps is limited; discharge-tube illumination, and most high-pressure sodium lamps, must be extinguished after midnight. Lamps must not emit light above the horizontal, so only the ~ 10% of the light reflected from the ground (snow does not fall on the streetlit parts of the island) escapes into the sky. Between 1992 and 1997, the estimated amount of light escaping into the sky has decreased by 20% as a consequence of an ongoing programme to improve the efficiency and shielding of public lighting (Javier Diaz, private communication). The V-band zenith sky brightness on La Palma is similar to that at other dark sites (Table 1), which suggests that light pollution must contribute <~ 0.1 mag to the total. Sky brightness is plotted against azimuth in Fig. 12. The raw data show considerable brightening in the south, but as can be seen from Fig. 12, this brightening disappears after the measuerments are corrected for the contribution of zodiacal light, and there is no discernible peak in sky brightness at any particular azimuth.
A much stronger limit on the contribution of light pollution to the brightness of the sky may be obtained from the equivalent widths of the NaD and Hg lines in the spectrum of the zenith night sky. These yield directly the contribution to sky brightness from emission lines, while that from broad and continuum features can be inferred from the strengths of the emission lines, the known shapes of the lamp spectra (given e.g. by Osterbrock 1976, and in the Philips Catalogue of Lamps), and the relative numbers of lamps of different kinds. The median equivalent widths of the NaD 5890/6, Hg 5460 and Hg 4358 A lines at solar minimum (when the continuum is faintest) during summer (when the airglow NaD is dimmest) are 100, 7 and 9 A respectively, although they vary by a factor of ~ 1.5, probably due to changing cloud cover below the observatory (as found at Palomar, see Turnrose 1974), which often blots streetlighting from view. The equivalent width shows no significant variation with zenith distance for ZD < 45o. Below are derived estimates of contamination in each of the bands U, B, V and R (negligible in I, where sky brightness is dominated by the OH airglow). The results are summarised in Table 4.
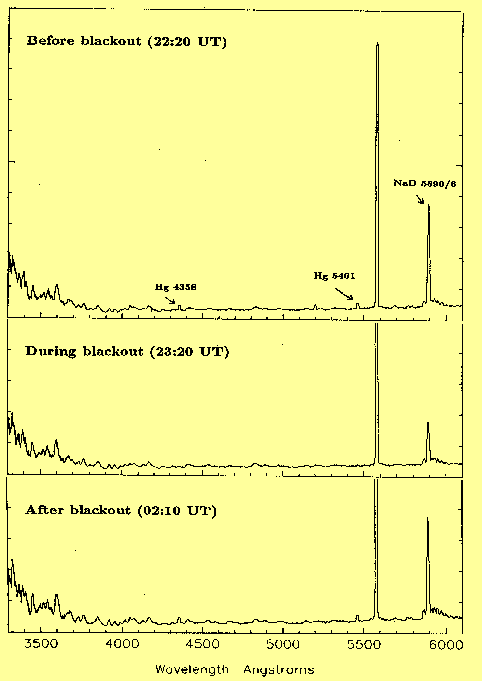
Low-presure sodium lamps An opportunity to separate the airglow and light-pollution NaD contributions arose on the night of 24/25 June 1995, when the Instituto de Astrofisica de Canarias arranged for most of the ~ 100000 street lamps on the four western Canary islands (La Palma, Tenerife, La Gomera and El Hierro) to be switched off for 1 hour starting at local midnight, to celebrate the 10th anniversary of the inauguration of the observatories. The observer at the William Herschel Telescope that night (Ian Waddington) happened to be taking near-zenith low-resolution spectra covering most of the visible range. From these it was possible to extract spectra of the moonless sky before, during and after the blackout (Fig. 13).
The equivalent widths of the NaD line before and during the blackout were 75 and 30 A respectively. At this wavelength, with the zenith sky brightness given in Table 2, an equivalent width of 30 A corresponds to 30 Rayleighs (see Appendix), in agreement with the 30 Rayleighs given by Allen (1973) for the summer strength of the NaD line. Thus, of the 100-A median observed equivalent width of the NaD line during the summer, ~ 70 A (70 Rayleighs) is due to street lighting, corresponding to an increase in sky brightness of ~ 0.04 mag in both V and R bands (equivalent width / bandwidth x relative filter transmission at 5893 A).
High-pressure sodium lamps
Mercury lamps
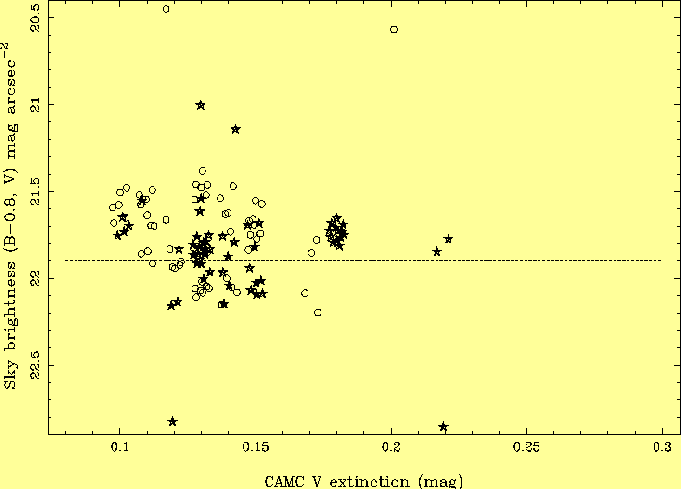
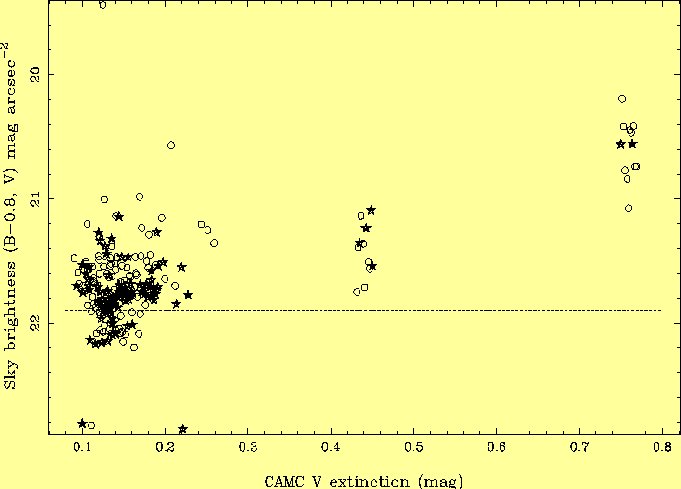
Incandescent lamps In summary, light pollution contributes < 0.03 mag to the zenith continuum sky brightness in all bands (Table 4), well below the IAU recommendation of < 0.1 mag at ZD = 45o, (see Section 1.5) for a dark observing site. The strength of the typical NaD 5890/6-A light pollution, ~ 70 Rayleighs, exceeds that due to natural airglow radiation (the limit recommended by the IAU for a dark site) during the summer. However, few spectroscopic observing programmes are likely to be adversely affected by this contamination. Streetlamp emissions in the Hg and NaD lines raise the broad-band V and R sky brightnesses by 0.09 and 0.08 mag respectively. The total contamination is < 0.03 mag in U, ~ 0.02 mag in B, ~ 0.10 mag in V, ~ 0.10 mag in R. This degree of light pollution is comparable to that at Kitt Peak, ~ 0.02 mag in B, 0.05 mag in V in 1988 (Massey et al 1990) from Tucson (275000 inhabitants, 65 km distant). It is less than that at Calar Alto, ~ 0.2 mag in V (Leinert et al 1995) from Almeria (160000 inhabitants, 45 km distant). It is more than that at La Silla, probably <~ 0.02 mag (Mattila et al 1996) from Vallemar (38000 inhabitants, 65 km away) and La Serena (160000 inhabitants, 150 km away). 3.7 Variation of sky brightness with extinctionOn La Palma, extinction is high during the summer months when a pall of neutral-extinction Saharan dust hangs over the islands (Whittet, Bode & Murdin 1987, Moulin et al 1997), see Figs. 3, 4. It is also high worldwide after large volcanic eruptions e.g. those of El Chichon (1982.2) and Pinatubo (1991.5). Dust will scatter and absorb light arising above the dust layer (e.g. airglow) or below it (e.g. street-lighting). The altitude of the dust layer is typically a few km, so that the total contributions of airglow and zodiacal light to the brightness of the sky will be diminished (although the scattering will redistribute the light); that of streetlighting may be increased or decreased.The change in sky brightness due to backscattering of streetlighting depends in a complex way on the size, space density and vertical distributions of the scattering species, on the distribution of streetlamps and on local topography (e.g. obscuring mountains) (Garstang 1989a,b, 1991a,b,c). However, a rough order-of-magnitude upper limit can be placed on the possible brightening of the sky due to this backscattering. We noted above that the intensities of eartbound light from the night sky, and of spacebound light escaping from street lamps, are similar, ~ 10 Wkm-2, so that if a large fraction of the streetlighting is back-scattered, the brightness of the sky could increase by a factor ~ 2, i.e. by ~ 1 mag. The relationship between extinction Av and brightening of the sky Delta may be predicted on the basis of an approximate model. About 0.1 mag of the total extinction on La Palma is due to atoms and molecules (King 1985), the rest (Av - 0.1) to dust. The dust is lower lying and is probably responsible for scattering back most of the street illumination which reaches the observatory. The intensity of the scattered light (proportional to 10Delta/2.5 -1) should be proportional to the fraction of starlight extinguished by dust (1-10-(Av-0.1)/2.5). Thus: Measured sky brightness is plotted against extinction Av (as recorded for the night by the Carlsberg Automatic Meridian Circle) in Figs. 14, 15. For Av < 0.25 mag, there is no significant variation (< 0.1 mag) of sky brightness with Av. Approximately 20% of nights on La Palma have Av > 0.25 mag, but our sample includes none satisfying the criteria given in the caption to Fig. 14, and when B, V measurements were made. Measurements were made from images taken at low ecliptic and galactic latitude on 21 August 1990 (INT, Av = 0.44 mag) and 13 June 1996 (JKT, Av = 0.76 mag), and the sky was markedly bright on both nights (Fig. 15). In part, this brightening is due to the lower ecliptic and galactic latitudes of the observations (Table 2), but the contributions from these effects are much smaller than the observed changes, and in the case of the 1996 data, similar measurements were obtained from the sky background on observations of high-latitude standard stars. On both nights, a similar number of measurements was made in both B and V bands, and the increases in sky brightness Delta B,V mag in the two bands are similar within the errors, Delta B,V ~ 0.3 mag (after correcting for the variation due to the solar cycle) at extinction 0.44 mag, Delta B,V ~ 1.4 mag at extinction 0.76 mag. Data are available in R band for June 1996, and the brightening is again ~ 1.4 mag. The brightening by 0.3 mag when Av = 0.44 mag implies that in the equation above, const = 1.0. This then predicts that for Av = 0.15 mag (median non-summer value), Delta ~ 0.06 mag, consistent with the observed value (0.10 mag) given in the last row of Table 4. For Av = 0.76 mag, on the other hand, the predicted brightening is only Delta = 0.5 mag, compared with an observed 1.4 mag. Clearly the model is naive for very large extinctions, possibly because the amount of dust close to the observatory does not vary in a simple way with the measured extinction of starlight. The similarity in Delta V and Delta R is consistent with the predictions of Table 4, since the contribution in both bands is determined mainly by the scattering properties of the dust at 5890/6 A. The similarity Delta B and Delta V is less easily explained, but the ratio is hard to predict, given the possible wavelength-dependence of the fraction scattered, and a probably changing mix of streetlamp types in the light scattered when the extinction is unusually high (the contribution from some towns may be blotted out). More detailed investigation of the effects of dust on sky brightness will be the subject of future work (maybe).
A correction has been made for the varying contribution of zodiacal light (see caption to Fig. 8).
3.8 Variation with season, lunar phase and weekdayDark-of-moon sky brightness does not vary significantly (<~ 0.1 mag) with season, lunar phase or weekday (possible effects mentioned in Section 1.1). A seasonal effect <~ 0.1 mag in V, R might be expected from the brightening of the airglow NaD line in winter. Tidal effects might drive a variation with lunar phase. A weekly variation might be driven by the reported weekly variation in the properties of the troposphere (Lenschow 1994, Gordon 1994) or by weekly cycles in use of artificial lighting.4.0 ConclusionsThe brightness of the moonless night sky above La Palma has been measured from 427 images taken with the Isaac Newton and Jacobus Kapteyn Telescopes during 1987 - 96. The broad-band sky brightness at high ecliptic and galactic latitudes and low airmass, at solar minimum, is given in various units in Table 5.Because of the significant equivalent widths of the emission lines in the airglow spectrum, the pseudo-continuum sky brightness in V,R seen by spectroscopists is ~ 0.2 mag fainter than the broad-band sky brightness seen by imaging observers.
Band wavel log10 Jy mag S_10 microJy ph R/A W/km^2
mic Hz mag0 "^-2 arcsec^-2 rate /ster
U 0.36 14.92 1810 22.0 205 2.87 0.012 0.64 1.02
B 0.44 14.83 4260 22.7 107 3.54 0.012 0.65 1.03
V 0.55 14.74 3640 21.9 224 6.33 0.017 0.93 1.47
R 0.64 14.67 3080 21.0 515 12.26 0.029 1.55 2.45
I 0.79 14.58 2550 20.0 1294 25.50 0.049 2.61 4.13
J 1.22 14.39 1570 16.6 29648 359.67 0.445 23.80 37.68
H 1.63 14.26 1020 14.4 224905 1772.56 1.640 87.80 138.98
K 2.19 14.14 640 12.0 2051163 10143.32 6.986 373.97 591.92
Table 5 -
La Palma dark-of-moon sky brightness is given in columns 5 - 10,
in various units (see Appendix
for details of the conversions).
The V sky brightness corresponds to ~ 59 nLamberts.
Approximate measurements in J,H, and K, from WHIRCAM on the
William Herschel Telescope, are included for convenience.
The K value includes an unknown thermal contribution from the telescope;
at UKIRT on Mauna Kea the measured K brightness is about 1.5 mag dimmer.
Columns 1, 2, 3 and 4 give the band name, wavelength in microns,
log10(frequency/Hz) and
the equivalent intensity in Jy for apparent mag = 0
(this last from Bessell 1979, Bessell & Brett J.M., 1988).
The units of column 8
(ph) are photons s-1m-2A-1arcsec-2.
The last column gives nu snu in Wkm-2ster-1.
The total sky brightnesses in the optical, in microwave-background
photons and
in cosmic rays,
are remarkably similar,
a few Wkm-2 each.
Some of the energy of the cosmic-rays
is converted to optical (Cerenkov) photons,
but they contribute only ~ 10-4 of the total sky brightnes
(Jelley 1958).
The sky brightness in V, R is similar to that at other dark sites.
In B the sky is measured to
be about 0.2 mag brighter than at other sites, but this may be because most
of the B data are drawn from 1995 when the B sky brightness was still
declining (Krisciunas 1997).
The V sky brightness on La Palma (and probably at other sites)
is given approximately (+- 0.1 mag) by the following formula
(reflecting the contributions listed in Table 2):
where with a small contribution (<~ 0.1 mag) from light pollution, much enhanced in the presence of extinction > 0.25 mag. The symbols are as given in Table 2. airmass approximates the van Rhijn factor given by the first equation in Section 1.7. The colour of the La Palma sky at solar minimum is B-V ~ 0.8, V-R ~ 0.9.
For sky-limited exposures, an uncertainty of 0.4 mag in the surface brightness of the night sky translates into an uncertainty of a factor of 2 in the exposure time required to reach a given signal-to-noise, with potential wastage of half that time. The measurements reported here of the absolute level of sky brightness, and of the ways in which it varies, allow more efficient use to be made of telescope time. AcknowledgmentsThis project was made possible by the existence of the comprehensive data archive of the Isaac Newton Group, and of the nightly record of extinction measured at the Carlsberg Automatic Meridian Circle. We are grateful to Ed Zuiderwijk (RGO) for helping us extract data from the archive, Javier Diaz (IAC) for making available information about street-lighting on La Palma, Roy Garstang (Colorado) for advice about the effects of dust, Simon Green (Kent) for drawing our attention to the importance of extragalactic fluctuations in the sky background, Matthew Wild (World Data Centre C) for making available the 10.7-cm solar flux-density record, Steve Bell (RGO) for providing a 10-year lunar ephemeris, and Max Pettini and Steve Maddox for measuring sky brightness during their observing runs. SLE carried out part of this work while a summer student at the Isaac Newton Group in 1996. This original version of this paper was prepared with LaTeX and PGPLOT.ReferencesAllen C.W., 1973, ` Astrophysical Quantities' 3rd edition (Athlone Press), p. 134Berry R.L., 1976, J. R. Astr. Soc. Canada, 70, 97 Bessell M.S., 1979, PASP, 91, 589 Bessell M.S. & Brett J.M., 1988, PASP, 100, 1134 Broadfoot A.L. & Kendall K.R., 1968, J. Geophys. Res., 73, 426 Burki G., Rufener F., Burnet M., Richard C., Blecha A., Bratschi P., 1995, AAS, 112, 383 CAMC, 1977, `Carlsberg Meridian Catalogue La Palma No. 9' (CD-ROM), Copenhagen University Observatory, Royal Greenwich Observatory, and Real Instituto y Observatorio de la Armada en San Fernando Chamberlain J.W., 1961, `Physics of the Aurora and Airglow' (New York: Academic Press), p. 517 Chatterjee T.N. & Das T.K., 1995, MNRAS, 274, 858 Cole S., Treyer M.-A., Silk J., 1992, ApJ, 385, 9 Crawford D.L., 1997, Observatory, 117, 14 Davies J.I., Disney M.J., Phillipps S., Boyle B.J., Couch W.J., 1994, MNRAS, 269, 349 Dumont R. & Levasseur-Regourd A.C., 1978, A&A, 64, 9 Forbes M.C.. Banks T., Sullivan D.J., Dodd R.J., Gilmore A.C., Kilmartin P.M., 1995, Observatory, 115, 29 Garcia-Rodriguez J.L. et al, 1990, `Atlas Interinsular de Canarias' (Club Canarias del Libro) Garstang R.H., 1984 Obs, 104, 196 Garstang R.H., 1986, PASP, 98, 364 Garstang R.H., 1988, Obs, 108, 159 Garstang R.H., 1989a, PASP, 101, 306 Garstang R.H., 1989b, Ann. Rev. Astron. Astrophys., 27, 19 Garstang R.H., 1991a, PASP, 103, 1109 Garstang R.H., 1991b, Obs, 111, 239 Garstang R.H., 1991c, in `Light Pollution, Radio Interference and Space Debris', ed. D.L. Crawford (PASP conference vol. 17), p.56 Geisler D., 1987, NOAO newsletter, 13, 22 Geisler D. et al, 1988, NOAO newsletter, 14, 24 Gordon A.H., 1994, Nature, 367, 325 Hogg D.W. et al, 1997, MNRAS, 288, 404 Holmes R.W., 1997, Observatory, 117, 25 Hunter T.B. & Crawford D.L., 1991 in `Light Pollution, Radio Interference and Space Debris', ed. D.L. Crawford (PASP conference vol. 17), p.89 Ingham M.F., 1962, MNRAS, 124, 505 Ingham M.F., 1972, Sc. American, Jan. 1972, p.78 James J.F., Mukai T., Watanabe T., Ishiguro M., Nakamura R., 1997, MNRAS, 288, 1022 Jelley J.V., 1958, `Cerenkov Radiation and its Applictions' (Pergamon Press 1958) Kalinowski J.K., Roosen R.G., Brandt J.C., 1975, PASP, 87, 869 Kaye G.W.C. & Laby T.H., 1973, Tables of Physical and Chemical Constants (Longman) King D.L., 1985, La Palma Technical Note 31, 'Atmospheric extinction at the Roque de Los Muchachos Observatory' Kordylewski K., 1961, Acta Astronomica, 11, 165 Krisciunas K., 1990, PASP, 102, 1052 Krisciunas K. & Schaefer B.E., 1991, PASP, 103, 1033 Krisciunas K., 1996, Sky & Telescope, February 1996, 91 Krisciunas K., 1997, PASP, 109, 1181 Landolt A.U., 1992, AJ, 104, 340 Leinert C., Pitz E., Hanner M., Link H., 1977, J. Geophys., 42, 699 Leinert C., Vaisanen P., Mattila K., Lehtinen K., 1995, AAS, 112, 99 Leinert C. et al, 1998, A&AS, in press Lenschow D.H., 1994, Nature 369, 193 Levasseur-Regourd A.C. & Dumont R., 1980, A&A, 84, 277 Lockwood G.W., Thompson D.T., Lumme K., 1980, AJ, 85, 961 Lockwood G.W., Floyd R.D., Thompson D.T., 1990, PASP, 102, 481 Longair M.S., 1993, QJRAS, 34, 157 Louistisserand S., Bucher A., Koutchmy S., Lamy P., 1987, AAS, 68, 539 Maihara T. et al 1993, PASP, 105, 940 Malin D., 1994, in `The Vanishing Universe - Adverse Environmental Impacts on Astronomy', ed. D. McNally (Cambridge University Press 1994), p.117 Massey P., Gronwall C., Pilachowski C., 1990, PASP, 102, 1046 Mattila K., Vaisanen P., v. Appen-Schuur G.F.O., 1996, AAS, 119, 153 McNally D., 1994, ed. `The Vanishing Universe - Adverse Environmental Impacts on Astronomy' (Cambridge University Press 1994) Mercer R.D., Drakelman L., Kinglesmith D.A., Alvord G.G., 1979, Space Res., 19, 467 Moulin C., Lambert C.E., Dulac F., Dayan U., 1997, Nature, 387, 691 Munoz-Tunon C., Vernin J., Varela A.M., 1997, AAS, 125, 183 Murdin P. 1985, Vistas Astr. 28, 449 Nawar S., Morcos A.B., Mikhail J.S., 1995, Earth, Moon and Planets, 70, 123 O'Connell R.W., 1987, AJ, 94, 876 Oliva E. & Origlia L., 1992, A&A, 254, 466 Osterbrock D.E., Walker M.F., Koski A.T., 1976, PASP, 88, 349 Osterbrock D.E., Fulbright J.P., Martel A., Keane M.J., Trager S.C., Basri G., 1996, PASP, 108, 277 Osterbrock D.E., Fulbright J.P., Bida T.A., 1997, PASP, 109, 614 Paresce F. & Jakobsen P., 1980, Nature, 288, 119 Pilachowski C. et al, 1988, NOAO newsletter no.15 p.14 Pilachowski C., Africano J.L., Goodrich B.D., Binkert W.S., 1989, PASP, 101, 707 Ramsay S.K., Mountain C.M., Geballe T.R., 1992, MNRAS, 259, 751 Roach F.E. & Gordon J.L., 1973, `The Light of the Night Sky' (Dordrecht: Reidel) Savage A., 1989, AAO newsletter 51 (10/89) Schneeberger T.J., Worden S.P., Beckers J.M., 1979, PASP, 91, 530 Shefov N.N., 1972, Ann. Geophys., 28, 137 Smith F.G., 1979, Trans IAU 17A, 220 Spinrad H., Stone R.P.S., 1978, ApJ, 226, 609 Stevenson C.C., 1994, MNRAS, 267, 904 Toller G., Tanabe H., Weinberg J.L., 1987, A&A, 188, 24 Treanor P.J., 1973, Observatory, 93, 117 Turnrose B.E., 1974, PASP, 86, 545 van Rhijn P.J., 1921, Publ. Astr. Lab. Groningen, No. 31, p.1 Vlasyuk V.V. & Spiridonova O.I., 1993, Astron. Rep., 37, 389 Walker M.F., 1970, PASP, 82, 672 Walker M.F., 1971, PASP, 83, 401 Walker M.F., 1973, PASP, 85, 508 Walker M.F., 1977, PASP, 89, 405 Walker M.F., 1988, PASP, 100, 496 Walker M.F., 1991, in `Light Pollution, Radio Interference and Space Debris', ed. D.L. Crawford (PASP conference vol. 17), p.52 Weinberg J.L., Sparrow J.G., 1978, `Cosmic Dust' (Wiley, New York), p.75 Wesson P.S., 1991, ApJ, 367, 399 Whittet D.C.B., Bode M.F., Murdin P., 1987, Vistas, 30, 135 Yocke M.A., Hogo H., Henderson D., 1986, PASP, 98, 889 Appendix - Light-intensity unitsAstronomers, airglow physicists and streetlight manufacturers use a variety of units for measuring light intensity. Some useful conversions are given below.
Physical units of surface brightness:
The lumen, used by lighting engineers, is a measure of luminous flux as perceived by the eye. An isotropic source of luminous flux 4pi lumens has a luminous intensity of 1 candela = 1 lumen ster-1, and this illuminates a surface 1 m away with illuminance E = 1 lux = 1 lumen m-2 = 10-4 phot. Luminance L measures light emitted or reflected by a surface, in lumens ster-1 m-2 (= cd m-2 = nit) (1 stilb = 1 cd cm-2, 1 lambert = 1/pi cd cm-2). Crawford (1997) gives a useful summary of these units and their interconversions. V = 21.9 mag arcsec-2 corresponds to 0.00019 cd m-2 equivalent to 59 nLamberts. Typical luminance values from Crawford (1997) and Holmes (1997): Surface L (cd m^-2) Dark night sky 0.0002 Sky at full moon 0.03 Lit road surface at night 0.5 Zenith at sunset 100 Surface of full moon 2500 Candle 10000 Surface of sun 1.6 x 10^9 A surface of luminance L cd m-2, subtending solid angle omega ster, yields an illuminance E = L omega lm m-2, e.g. for the sun, L = 1.6 x 109 cd m-2, omega = 7.7 x 10-5 ster, E = 1.2 x 105 lum m-2. Note that the values of L, whose units are lm ster-1 m-2, can be interpreted in two equivalent ways: as the number of lumens emitted into each steradian by each m2 of a luminous surface, or as the number of lumens received by each m2 of a surface from each steradian subtended by an emitter. At 5550 A, 1 W ~ 680 lumens (Kaye & Laby 1973). On La Palma, the streetlamps (typically emitting a few thousand lumens each) produce an average of 63 lumens per W of electrical power supplied by the lamp control gear. Approximately half the lumens emitted escape from the lamp housing, and about 10% of the latter are reflected upwards by the ground. Go to La Palma site-quality page Minor changes occasioned by converting original document to html: Greek characters (lambda, omega, pi, tau) and symbols (sun, equivalent to) replaced by words; ~ substitutes for both 'approx' and 'of order'; footnotes reformatted; equation numbers and accents have vanished. No changes have been made to the technical content.
|