Sensitivity
The "limiting magnitude" of an IR instrument can be easily
predicted when the observations are taken in the
background-limited
case (i.e. the readout noise is
negligible compared to the background shot noise).
From the
zeropoints
and the background brightnesses in J, H and Ks, we have calculated
the expected limiting magnitude as a function of: (i) the exposure
time, (ii) the seeing (for point sources) and (iii) the required signal
to noise ratio.
You should bear in mind that the background brightness is highly
variable, so that the
calculated limiting magnitude can vary from night to night - see the
plots
of limiting
magnitudes for point sources and extended sources.
The limiting magnitudes have been calculated using the equation
(McLean 1997)

This equation assumes that observations are taken in the background limited case, where
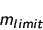 |
is the predicted limiting
magnitude. |
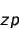 |
is the zeropoint of the
instrumental scale (i.e. the magnitude of a source that gives a flux of
1 ADU/s). |
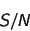 |
is the signal to noise
ratio for the detection of the limiting magnitude. |
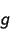 |
is the gain (in e-/ADU)
of the detector. |
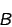 |
is the background signal
per pixel (in e-/s/pix). |
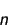 |
is the
number of pixels covered by a point source. We assume that
n=pi*(seeing/0.238)2 ie. the source radius is equal to the
seeing (fwhm), which is probably pessimistic. For extended objects, the
limiting magnitude per
arcsec2 has been given instead i.e. n=1/0.2382.
|
 |
is the total on-object
integration time (ie. the number of object frames × exposure time
of each individual frame). |
From the formula above, it can be seen that if the background
increases by a factor of 2, the limiting magnitude in the plots would
decrease by ~0.38 mag (or ~0.38 mag/arcsec²
for extended objects). In order to reach the same limiting magnitude,
one would need to increase the total on-object exposure time by a
factor of 2.
If the seeing were to deteriorate by a factor of 2, the limiting
magnitudes in the plots would decrease by ~0.75 mag. Consequently, the
total on-object exposure time
would have to be increased by a factor of 4 to reach the same limiting
magnitude.
If a S/N of 5 (instead of 3) were required, the limiting magnitudes in
the plots would decrease by ~0.55 mag. In order to reach the same
limiting magnitude,
one would need to increase the total on-object exposure time by a
factor of ~2.8.
Note that you can also use the exposure time calculator
SIGNAL to calculate the number of photons (from both the object and
the sky) that will be detected during an INGRID exposure of a point or
extended source.

