| |||
|
| Home > Astronomy > Filters > Calculation of Central Wavelength |
Calculation of Central Wavelength
The effective central wavelength of a given filter can be different from the value listed at the filter database. See below a description of the various effects that can change the central wavelength and use this central wavelength shitft calculator.
Nominal central wavelength and error estimateNote that in most cases the filter scanner used to measure the central wavelengths provided on the ING filter database, uses a rectangular beam of light to measure the throughput. In one dimension this beam has a f/9.0 focal ratio, in the other dimension it has f/26.1. For interference filters this will affect the measured central wavelength. As an approach, a wavelength error can be estimated as follows:
Or ~0.02% the nominal central wavelength value. For instance, at λ0=6330Å error is +0-1.1Å. We recommend observers contact ING Filters if they are unsure of the nominal and the effective central wavelength values. Change due to ray of light incident at a specific angle to the normalWhen interference filters are used at angles other than normal incidence, the optical path difference between the direct transmitted beam and the multiple order reflections within the cavity decreases, causing a corresponding decrease in the wavelength of peak transmission. Changes in the bandwidth and transmission characteristics are generally small (for the relatively wide passbands used here). For angular tilts of less than 10°, the central wavelength can be calculated from the expression
where
and n = the refractive index of the interference coatings of the filter.
Change due to uncollimated lightUtilising the filter in uncollimated (i.e. convergent or divergent) light involves slightly more complex considerations. Here, light enters the filter at a range of angles, so that different rays undergo unequal wavelength shifts. This results in not only a central wavelength shift, but a broadening of the bandwidth and lower peak transmission. As a rough approximation, relatively uniform beams (with semi-cone angles greater than 5°) will undergo peak shifts of aproximately one half of that which would be predicted for a collimated beam at the maximum angle of incidence of the cone.
The focal ratio of the INT prime focus is 3.29, which gives a maximum angle
of incidence of the cone (semi-cone angle) of
Therefore, at the INT prime focus, the central wavelength (i.e. the wavelength
of peak transmission) is shifted towards shorter wavelengths by 0.13% from the
measured central wavelength in a collimated beam.
For example, for an
Similarly for the WHT prime focus the maximum cone angle (semi-cone angle) is
Change due to temperatureTemperature changes affect a filter's performance due to thermal expansion and contraction of the materials used to construct them. Most filters are designed and specified for operating at 23°C, and deviations from this value will produce peak wavelength shifts approximately linear with temperature. The exact shift coefficient will depend on the particular design wavelength of the filter, and, typically, ranges between 0.15Å and 0.20Å per °C at 4000Å and 8000Å respectively. Bandwidth and peak transmission changes observed are relatively minor, of the order of 0.01Å per °C and 0.013Å per °C respectively.
More information
|
| Top | Back |
|

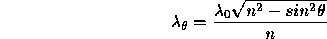
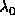 = Central wavelength at normal incidence
= Central wavelength at normal incidence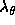 = Central wavelength at the off-normal
angle,
= Central wavelength at the off-normal
angle, 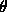
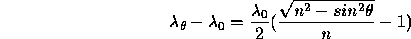
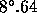 , so, substituting again into
the equation,
, so, substituting again into
the equation,

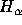 filter
with specified central wavelength 6558Å, the effective central wavelength
will be 6549.6Å.
filter
with specified central wavelength 6558Å, the effective central wavelength
will be 6549.6Å.
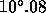 ,
and the central wavelength is shifted towards shorter wavelengths by
0.17% from the measured
central wavelength in a collimated beam.
,
and the central wavelength is shifted towards shorter wavelengths by
0.17% from the measured
central wavelength in a collimated beam.