 INS-DAS-19:
INS-DAS-19: Coordinate systems for UltraDAS
 INS-DAS-19:
INS-DAS-19: UltraDAS handling of geometry draws heavily on conventions developed at NOAO. This document rephrases the work published by NOAO for clarity, and explores areas of the problem that were not considered by NOAO.
The amplifier, CCD, detector and image coordinates were defined and named by NOAO defined and named by NOAO [1] . "Linear coordinates" and "readout coordinates" are new names chosen for UltraDAS.
A multi-channel camera has exactly one system each of linear and detector coordinates. It has separate amplifier and readout coordinate-systems for each amplifier in play. It has one system of CCD coordinates for each physical detector-chip. It has one set of image coordinates for each separate image it produces. That is, a four-quadrant camera with the quadrants reassembled before output has one set of image coordinates and a four-chip mosaic that produces four rasters per output file has four sets of image coordinates.
All pixel coordinates have integral values at the centre of a pixel. The detector coordinates ignore misalignments between the detector chips: the chips are treated as if the the rotations between their separate CCD coordinate-systems are exact multiple of 90 degrees and as if the gaps between chips are exact multiples of one pixel. UltraDAS assumes that all pixels are square.
Amplifier, CCD and detector coordinates are in unbinned pixels. Image and readout coordinates are in binned pixels.
Detector coordinates are defined to be a right-handed Cartesian system if one looks along the light beam towards the detector surface. For UltraDAS, CCD coordinates are always chosen to have the same parity as detector coordinates. Amplifier coordinates may have either parity with respect to detector coordinates, depending on where the amplifier was on the detector chip. Readout coordinates always have the same parity as the associated amplifier coordinates. The handedness of the linear coordinates is still under discussion. The parity of image coordinates is arbitrary and can be chosen by the programmer. There is advantage in setting up the system so that North is at high y and East is at high x (for direct imaging) or so that wavelength increases with x (for slit spectroscopy).
CCD coordinates assign the first and second coordinate according to the "natural" orientation of the chip. For example, on an EEV42 CCD, the first or x coordinate is naturally along the short axis of the chip and the two output amplifiers are at the low-y end; pixel (1,1) is next to the left-hand amplifier. For a square CCD with one amplifier, pixel (1,1) is next to the amplifier. For INGRID, a four-quadrant device, quadrant 1 is chosen arbitrarily and pixel (1,1) in CCD coordinates is next to the amplifier of quadrant 1. This means that CCD coordinates may be rotated with respect to detector coordinates, as in chip 2 of the INT WFC.
Amplifier and readout coordinates take the axis of serial clocking as the first coordinate and the axis of parallel clocking as the second. The coordinates increase in the opposite direction to the movement of charge towards the amplifier.
In amplifier coordinates, the first physical pixel has coordinates (1,1). Underscan and overscan areas are treated as extensions of the physical raster. Hence, underscan pixels often have negative amplifier coordinates.
In the detector coordinates of a mosaic, the physical pixels of different chips are assigned coordinates that best describe their position in the focal plane: that is, the detector coordinates take account of gaps between chips. Underscan and overscan areas are treated as extra pixels next to the physical pixels, i.e. inside the gaps. Often, the width of a gap is less than the width of underscan and overscan "in" that gap. When this happens, the adjacent underscan and overscan areas overlap in detector coordinates.
Image cubes may be created in any of the coordinate systems, but most
commonly in the image coordinates. The third co-ordinate has no geometric
relation with the image plane defined by the first two coordinates; rotation
of other axes into that plane is meaningless and is always an error. The
third co-ordinate may represent a continuous quantity - time of observation
is most common - but the planes need not be evenly spaced along the axis.
IRAF has a well-established notation for an image section: [x1:x2,y1:y2] defines the image section from x1 to x2, inclusive in the first coordinate and from y1 to y2, inclusive, in the second coordinate. If an image has X by Y pixels in total, the section [1:X,1:Y] is the whole image. UltraDAS uses this notation widely. The IRAF notation needs to be qualified by a note of which coordinate system the section is expressed in.
Readout windows, overscan and underscan regions can all be expressed as sections. The size of a whole chip can also be expressed this way.
UltraDAS has a naming convention for certain special image-sections.
The amplifier section is the set of physical pixels read from a
particular amplifier. The CCD section is all the physical pixels
in the chip in question. The readout section is all the pixels,
underscan, physical and overscan read from a particular amplifier.
p' = Rp + d
where the tensor R expresses differences in orientation and scale and the vector d expresses the displacement between the origins of the two coordinate systems.
Further, R can be factored into three stages
R = F T S
where F ("flip") expresses a possible reversal of the x-axis, T ("twist") expresses rotation about the origin and S ("stretch") expresses the difference in coordinate intervals. Clearly, these stages could be done in a different order (in which case the tensors would take different values), but UltraDAS uses the order FTS as an internal standard. (This ordering is important because UltraDAS requires the F , T, S components of some mappings to be specified in configuration files.)
Where there are two successive mappings specified by R1, d1 and R2,d2, these can be combined algebraically:
p" = R2p'+d2 = R2 (R1p+d1)+d2 = R2R1p+R2d1+d2
and this operation can be extended to chains of three or more mappings. This is important for UltraDAS because it avoids manipulating the pixels of a large image more than once.
It is useful to express all all coordinate systems in terms of a mapping from the system in question to a standard or central system: for UltraDAS, the latter system is detector coordinates. This means that the mapping between two systems is made up of two separate mappings, one applied in the forward direction and one in the reverse.
Given R and d, the reverse mapping is
p = R-1(p'-d) = R'p' +d'
where
R' = R-1 = S-1T-1F-1
and
d' = -R'd .
The composition of R' may be deduced from considering a mapping with d = 0 in which applying each consituent of R in turn generates the mapping and applying the inverse of those operations in the reverse order reverses the whole mapping. It is also useful to note that F-1 = F.
Thus, if we have coordinates p1 in space 1, for which R1 and d1 map to detector coordinates, and coordinate p2 in space 2, for which R2 and d2 map to detector coordinates,
p2 = R'2R1p1 + R'2d1 + d'2 = R'2R1p1 + R'2(d1 - d2) = R"p1 + d"
This latter mapping is the form that the UltraDAS software actually uses.
A special case is mapping a region of pixels onto itself with the new origin at a different position. Here, it is important to remember that although the raster has not moved, the origin has, so d is non-zero.
If an image section is expressed in binned readout co-ordinates, then
its pixels are larger than those in detector co-ordinates; i.e. one binned
pixel in readout co-ordinates occupies more than one pixel in detector
co-ordinates. This means that the scale factors in the mapping are greater
than one when mapping from readout co-ordinates to detector co-ordinates,
and less than one when mapping the other way.
The result is mathematically valid, but it breaks the convention on the use of i-space: the first pixel in an output image is defined to lie at (1,1) in i-space. To fix this, the origin of the i-space is changed to bring the first pixel to (1,1) in the revised space: this is referred to as normalising i-space.
Normalisation is done for every image output by UltraDAS.
These aspects of geometry are set in the configuration files:
Each of the xspace statements gives a mapping in this format:
<parity> <rotation> <x-scaling> <y-scaling> <x-offset> <y-offset>
where
For aspace, ispace and rspace, the scale factors
must always exactly one (i.e. the spaces are for unbinned pixels) and the
rotation must be in steps of exactly 90 degrees. The displacement is in
pixels.
The main "customer" for WCS data at ING is the WFS survey programme, producing imaging data with the Wide-Field Camera at the the prime focus of the INT. The best mapping to the sky for these data is "tangent-plane" or "gnomonomic" projection with a radial, cubic correction term. The parameters of this projection also work well for the prime focus of the WHT and at least moderately well for all direct-imaging cameras. The encoding of Greisen and Calabretta [4], [5] is used.
The placeholder cards have to take some value. UltraDAS uses them to describe the mapping from i-space to d-space. That is, the units are made pixels, the axis types are made "X" and "Y", and the other values are filled in as necessary. The linear term of the projection is set to one and the cubic term to zero; this means, effectively, "no projection effects apply". The use of d-space means that a WCS-aware image-display will be able to mosaic together the separate images form a multi-channel camera.
NOAO also record in FITS cards the transformation matrices for mapping
between the amplifier, CCD, detector and image coordinate-systems. These
mappings are effectively additional WCSes for the image coordinate-system,
but expressed in a form very different to the emerging FITS-standard for
a WCS. Clearly, being able to map output images to the other coordinate
systems is useful. However, it is unclear whether software is available
to ING that uses NOAO's encoding, so UltraDAS does not write these keywords.
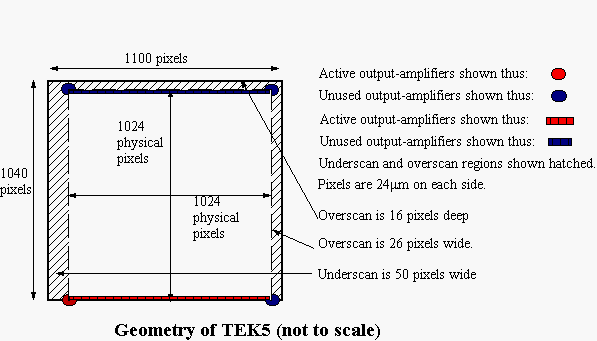
The amplifier is at the bottom left-hand corner of the chip and amplifier coordinates are right-handed. Amplifier, CCD and detector coordinates are identical; image coordinates are offset due to the underscan.
TEK5 is the prototype for all ING's Tektronix CCDs.
In the configuration file:
1 ampsize 1100 1040 1 biassec [10:50,2:1039] [10:1099,1027:1039] [1081:1099,2:1039] [0:0,0:0] 1 trimsec [53:1078,1:1024] 1 rspace +1 0 1 1 0 0 1 aspace +1 0 1 1 50 0 1 ispace +1 0 1 1 0 0
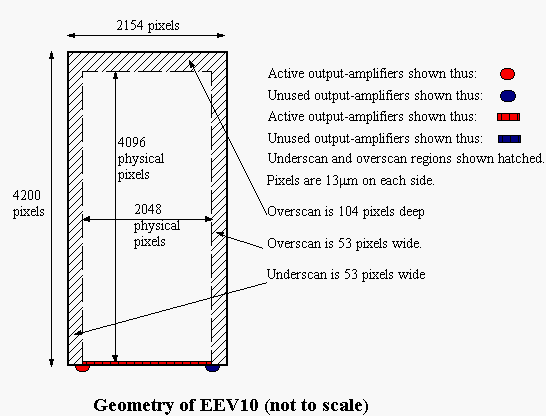
EEV10 has an EEV42 CCD which is read from the left-hand amplifier. ING has other cameras of this type.
The chosen amplifier is at the bottom left-hand corner of the chip and amplifier coordinates are right-handed. Amplifier, CCD and detector coordinates are identical; readout and image coordinates are offset due to the underscan. Linear coordinates have the origin at the centre of the chip (because this is approximately on the rotator centre for most instruments) and are aligned to detector coordinates.
EEV10 is usually used on IDS, with its long axis along the dispersion direction. The standard orientation involves rotating the output image clockwise by 90 degrees to get wavelength increasing to the right. Standard orientation is the default for IDS.
The bias is taken from the y-overscan. The first and last few columns of EEV42 readout tend to be corrupt, so these are avoided.
EEV10 is the prototype for all ING's single-EEV42 cameras that use the left-hand amplifier only.
1 ampsize 2154 4200 1 trimsec [54:2101,1:4099] 1 biassec [10:50,5:4190] [10:2150,4105:4190] [2110:2150,5:4190] [0:0,0:0] 1 rspace +1 0 1 1 0 0 1 aspace +1 0 1 1 53 0 1 ispace +1 0 1 1 0 0
1 ampsize 2154 4200 1 trimsec [54:2101,1:4099] 1 biassec [10:50,5:4190] [10:2150,4105:4190] [2110:2150,5:4190] [0:0,0:0] 1 rspace +1 0 1 1 0 0 1 aspace +1 0 1 1 53 0 1 ispace +1 0 1 1 0 0
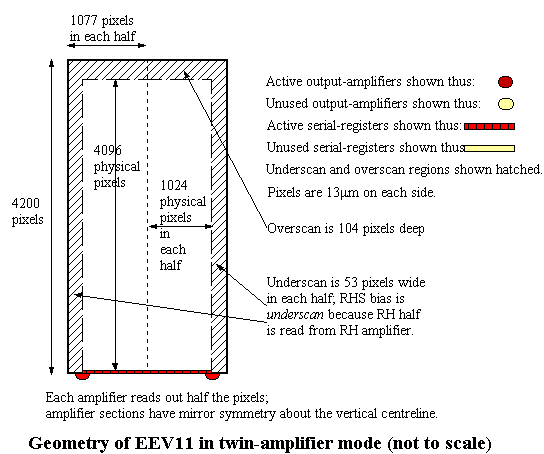
EEV11 has an engineering-grade EEV42 CCD. It has been used to demonstrate readout from both amplifiers in parallel, and the configuration here reflects that. If EEV11 is read from the left amplifier only, then its configuration would be as for EEV13.
All the remarks about the silicon for EEV13 apply to EEV11 as well.
The difference is that exactly half the data goes to each amplifier and
the two amplifiers produce sections with opposite parity of coordinates.
1 ampsize 1077 4200 1 ampsec [54:1077,1:4096] 1 trimsec [54:1077,1:4096] 1 biassec [15:1077,4101:4200] 1 rspace +1 0 1 1 0 0 1 aspace +1 0 1 1 53 0 1 ispace +1 0 1 1 0 0
2 ampsize 1077, 4200 2 ampsec [54:1077,1:4096] 2 trimsec [1:2154,1:4096] 2 biassec [1:1062,4101:4200] 2 rspace -1 0 1 1 2154 0 2 aspace -1 0 1 1 2101 0 2 ispace +1 0 1 1 0 0
1 readsec [1:1077,1:4200] 1 ampsec [54:1077,1:4096] 1 biassec [15:1077,4101:4200] 1 rspace +1 0 1 1 0 0 1 aspace +1 0 1 1 53 0 1 ispace +1 0 1 1 0 0
2 readsec [1:1077,1:4200] 2 ampsec [54:1077,1:4096] 2 trimsec [1:2154,1:4096] 2 biassec [1:1062,4101:4200] 2 rspace +1 0 1 1 2088 -4 2 aspace +1 0 1 1 2033 -4 2 ispace +1 0 1 1 0 0
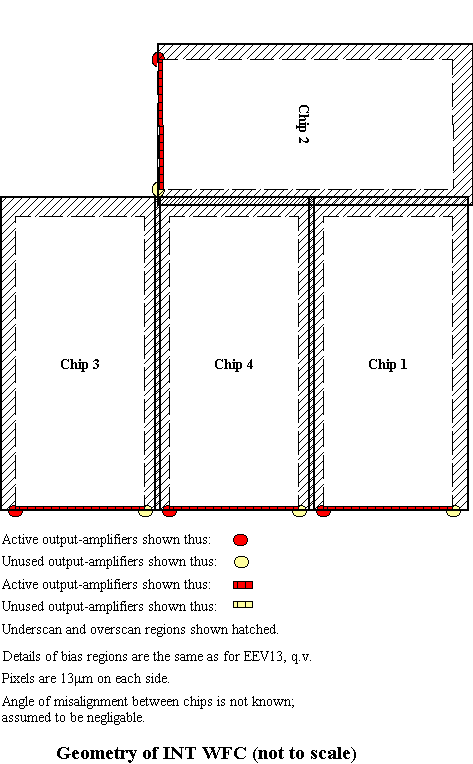
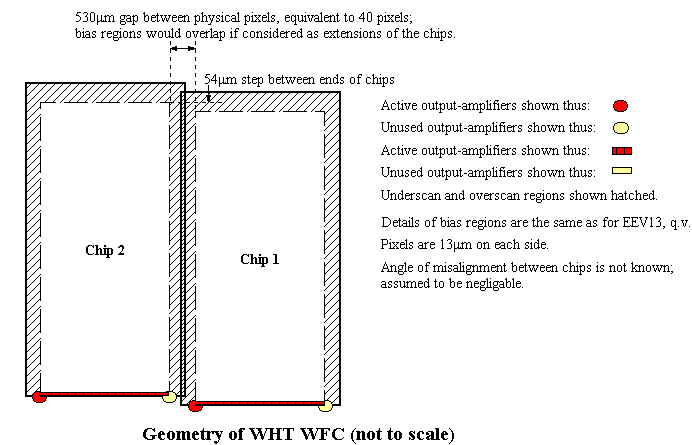
The INT Wide-field camera has four EEV42 CCDs arranged as in the diagram above. The CCDs are read out in the same way as EEV13.
Detector coordinates are aligned with chips 3, 4 and 1, and have the same origin as chip 4's amplifier coordinates.
Developers have been told by the WFS team not to mess around with the data orientation, on pain of death. Hence, i-space is the same as r-space for each chip.
1 ccdname A5506-4 1 ampname LH 1 chiptype EEV42-80 1 ampsize 2154 4200 1 aspace +1 0 1 1 2114 12 1 rspace +1 0 1 1 2061 12 1 ispace +1 0 1 1 2061 12 1 rogain 2.8 2.8 1 ronoise 3.9 3.9 1 biassec [10:50,5:4190] [10:2150,4105:4190] [2110:2150,5:4190] [0:0,0:0] 1 trimsec [54:2101,1:4096] 2 ccdname A5383-17-7 2 ampname LH 2 chiptype EEV42-80 2 ampsize 2154 4200 2 aspace +1 -90 1 1 91 6232 2 rspace +1 -90 1 1 38 6232 2 ispace +1 -90 1 1 38 6232 2 rogain 2.8 2.8 2 ronoise 4.6 4.6 2 biassec [10:50,5:4190] [10:2150,4105:4190] [2110:2150,5:4190] [0:0,0:0] 2 trimsec [54:2101,1:4096] 3 ccdname A5530-3 3 ampname LH 3 chiptype EEV42-80 3 ampsize 2154 4200 3 aspace +1 0 1 1 -2089 25 3 rspace +1 0 1 1 -2142 25 3 ispace +1 0 1 1 -2142 25 3 rogain 2.4 2.4 3 ronoise 3.7 3.7 3 biassec [10:50,5:4190] [10:2150,4105:4190] [2110:2150,5:4190] [0:0,0:0] 3 trimsec [54:2101,1:4096] 4 ccdname A5382-1-7 4 ampname LH 4 chiptype EEV42-80 4 ampsize 2154 4200 4 aspace +1 0 1 1 0 0 4 rspace +1 0 1 1 -53 0 4 ispace +1 0 1 1 -53 0 4 rogain 2.8 2.8 4 ronoise 3.9 3.9 4 biassec [10:50,5:4190] [10:2150,4105:4190] [2110:2150,5:4190] [0:0,0:0] 4 trimsec [54:2101,1:4096]Note on the data above: the positions of the amplifier sections were derived from the "virtual pixel coordinates" derived by Jim Lewis and Mike Irwin [private communication]. These are an extension of the amplifier coordinates of chip 4, which I have here chosen as detector coordinates. The relative positions of the chips were found by astrometry. The alignment of chip 4 with North is not currently known to me. I have assumed for the sake of example that it is exactly aligned. The relative alignments of the chips are derived from the astrometry.
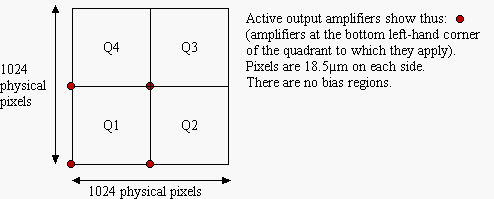
The CCD co-ordinates and detector co-ordinates are the same; they are aligned with and share the origin of the amplifier co-ordinates in quadrant 1. Due to lack of underscan, readout and amplifier co-ordinates are identical for any given quadrant.
1 ccdname INGRID 1 ampname quadrant-1 1 ampsize 512 512 1 aspace +1 0 1 1 0 0 1 rspace +1 0 1 1 0 0 1 ispace +1 0 1 1 0 0 1 trimsec [1:512,1:512] 2 ccdname INGRID 2 ampname quadrant-2 2 ampsize 512 512 2 aspace +1 0 1 1 512 0 2 rspace +1 0 1 1 512 0 2 jointo 1 2 trimsec [1:512,1:512] 3 ccdname INGRID 3 ampname quadrant-3 3 ampsize 512 512 3 aspace +1 0 1 1 512 512 3 rspace +1 0 1 1 512 512 3 jointo 1 3 trimsec [1:512,1:512] 4 ccdname INGRID 4 ampname quadrant-4 4 ampsize 512 512 4 aspace +1 0 1 1 0 512 4 rspace +1 0 1 1 0 512 4 jointo 1 4 trimsec [1:512,1:512]