| THE ING NEWSLETTER | No. 5, October 2001 |
|
|
SCIENCE |
|
|
|
| Previous: | NAOMI News | Up: | Table of Contents | Next: | The ING Red Sensitive CCD Project |
Other available formats: PDF
First Light on the New Small Fibre Module of Autofib2/WYFFOS
R. L. M. Corradi, K. M. Dee, R. A. Bassom, M. F. Blanken, S. J. Goodsell and M. van der Hoeven (ING)
Autofib2/WYFFOS
is the multi-object, wide field fibre spectrograph working at the prime
focus of the William Herschel Telescope. At the prime focus, the fibres
are placed onto a field plate by the robot positioner Autofib2 (AF2) at
user-defined sky coordinates. Object light collected at prime is transmitted
along fibres 26 metres in length to the Wide Field Fibre Optical Spectrograph
(WYFFOS). The path from prime focus to the spectrograph consists of a prism,
fibre button, 26 metres of fibre, finger, microlens and the facet block.
At the end of July 2001,
a major upgrade of the instrument was performed by successfully installing
the new Small Fibre Module of AF2. With the new fibres, AF2 can presently
observe up to 150 science targets over a field of 1 degree diameter (with
an unvignetted field of 40 arcminutes). Each of the 150 science fibres
has a diameter of 1.6 arcsec (90 micron), and runs without connectors from
AF2 to WYFFOS. The fibres are high-content OH fused silica made by Polymicro.
 |
 |
| Figures 1 and 2: Top [ JPEG | TIFF ] and side [ JPEG | TIFF ] views of a fibre prism and gripper button. | |
The small fibres replace the Large Fibre (2.7 arcsec diameter) Module, and have the following two main advantages:
i) No light is lost because of fibre connectors, providing a much more homogeneous distribution of fibre relative throughput as compared to the large fibres, and a higher mean throughput.
ii) The sky/background contribution
in observations with the small fibres is 3 times lower than with the large
fibres. This means that, with the small fibres, the noise level in sky-limited
observations is down by a factor of 0.6. The 1.6 arcsec diameter was chosen
as a the optimal compromise between minimum sky contribution and maximal
source contribution under good seeing conditions.
 |
 |
 |
|
| Figure 3 (left). Alignment of fibres into micro-lens finger holder [ JPEG | TIFF ]. Figure 4 (top right). Fingers mounted onto the facet block [ JPEG | TIFF ]. Figure 5 (bottom right). The Small Fibre Module at WHT prime focus [ JPEG | TIFF ] | |
At the spectrograph focus, the small fibres are imaged onto less than 2 pixels (FWHM) on the TEK6 detector in the spatial and spectral directions. The full spatial image of the fibres is therefore sampled by less than 3 pixels. The fibre distance in the WYFFOS entrance slit is 1 mm, which transforms onto a peak-to-peak aperture distance of 6-7 pixels on the detector. Although the nominal spectral resolving power has increased as the ratio of large to small fibre diameters, the actual resolution is limited by the CCD pixels, because of the undersampling along the spectral direction. WYFFOS can achieve dispersions as high as 0.8 Å/pixel with the 2400 line grating with the present TEK CCD with 24 micron pixels. With the WYFFOS echelle grating the dispersion ranges from 0.24 Å/pixel to 0.57 Å/pixel.
With the Small Fibre Module, 10 new fiducial imaging bundles are available for field acquisition and guiding. Each imaging bundle (450 micron diameter) contains 10,000 individual fibres providing a rough imaging capability over a 8 arcsec round field. The new coherent bundles also allow for autoguiding.
In July 2001, we obtained
the first measurements of the relative and absolute throughput of the science
fibres. As mentioned above, the distribution of relative throughput is
much more homogeneous than for the large fibres, and most fibres lie in
the region within 15% from the median throughput. The absolute throughput
of the small fibres was measured using grating R600B, under variable seeing
conditions of 1-1.3 arcsec. Table 1 reports the magnitude
of a star giving 1 electron/sec/Angstrom when observed at zenith. Numbers
are scaled to the "median" fibre (i.e. to the median relative throughput).
|
||||||||||||
| Table 1. Magnitude of a star giving 1 electron/sec/Angstrom when observed at zenith. |
These figures are similar to those measured in the past for the best large fibres, implying a substantial gain with respect to all those large fibres that had a much lower throughput because of light loss in the connectors.
The Small Fibre Module is currently being offered to observers. More information about AF2 can be found in our web pages at: http://www.ing.iac.es/Astronomy/instruments/af2/
In spite of the successful commissioning, quite a lot of work is needed in order to improve and fully characterise the performance of AF2 and its new fibres. Further enhancements to the system are planned. A major improvement will be the introduction of the WYFFOS long camera. This will give twice the spectral resolution of the current camera, allowing us to increase the number of fibres on the chip. The long camera is under construction and is expected to become available at the WHT at the end of 2002.
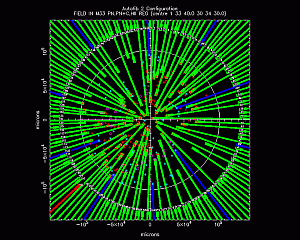 |
| Figure 6. Example of a science fibre configuration on the nearby galaxy M33. The science fibres are shown in green (in red a fibre that was temporarily disabled), and the fiducial bundles in blue. Targets are the red crosses, while light-blue stars are fiducial stars for acquisition and guiding. The white circle shows the usable field of view (1 degree diameter). [ GIF | TIFF ] |
Finally, we would like to
acknowledge all people who took part in the various stages of the development
of AF2, and in particular Mariet Broxterman, Nick Ferneyhough, Robert Greimel,
Steve Magee, Neil O'Mahoney, Roberto Martínez, John Telting, Bart
Van Venroy and Sue Worswick.
Email contact: Romano Corradi (rcorradi@ing.iac.es)
| Previous: | NAOMI News | Up: | Table of Contents | Next: | The ING Red Sensitive CCD Project |
| GENERAL | SCIENCE | TELESCOPES AND INSTRUMENTATION | OTHER NEWS FROM ING | TELESCOPE TIME |