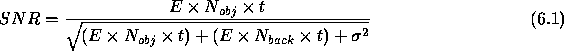



Probably the most important criterion in choosing a detector is the achievement of the required signal to noise ratio in the shortest integration time. The first step is therefore to define what signal to noise ratio is required for the observation to be successful. Having done that, we need to consider how to obtain this signal to noise ratio most efficiently.
The noise level for a typical astronomical observation will consist of three components. The first component is signal independent noise arising from the detector itself, readout noise in the case of a CCD and dark counts in the IPCS. Secondly, we have shot noise in the signal from the object being observed. This follows a Poisson distribution, so its variance is equal to the signal level. Finally, we also have shot noise in any background signal (particularly the sky background). Adding the noise terms in quadrature, the signal to noise ratio (SNR) is given by:
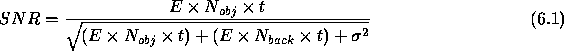
E = Responsive quantum efficiency of the detector *= Number of photons per resolution element per second incident on detector * from object *
= Number of photons per resolution element per second incident on detector * from background (e.g. sky) * t = Integration time *
= Detector noise (readout noise, dark current)
The signal to noise ratio obtained therefore depends on both the efficiency of the detector and the level of detector noise. The way to choose the optimum detector is therefore to choose the combination of efficiency and detector noise which maximises the signal to noise ratio. The two detector types are complementary in this respect, since the IPCS has the lowest level of detector noise but is also the least efficient, the (thinned) CCDs are the most efficient detector but also have a finite noise level. We now quantify these statements more precisely.
Table  gives estimates of the efficiencies of some representative detectors
at a number of wavelengths, using data taken from Sections
gives estimates of the efficiencies of some representative detectors
at a number of wavelengths, using data taken from Sections
 and
and  .
.
The detector noise of a CCD is dominated by the readout noise. Note however that the number we really need is the readout noise per resolution element, not the readout noise per pixel. The readout noise per resolution element depends on two factors:
 can be used to estimate the total integration time
required for a given telescope and instrument.
If the total integration time is greater than about 1 hour, it
will be necessary to split the observation into a number of shorter
exposures. Each CCD exposure adds in more
readout noise, resulting in the effective detector noise being equal
to the readout noise per exposure times the square root of the number
of exposures.
can be used to estimate the total integration time
required for a given telescope and instrument.
If the total integration time is greater than about 1 hour, it
will be necessary to split the observation into a number of shorter
exposures. Each CCD exposure adds in more
readout noise, resulting in the effective detector noise being equal
to the readout noise per exposure times the square root of the number
of exposures.
The detector noise of the IPCS comes from the dark count, which is so small that we can neglect it at all practical light levels.