JOSE Seeing Measurements

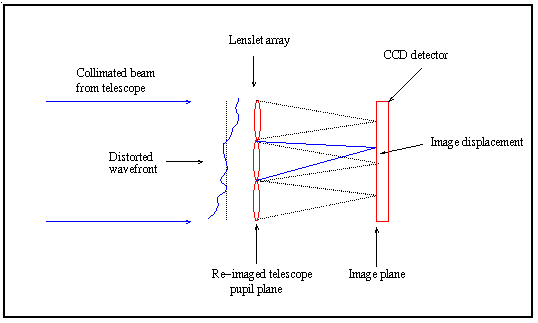
The pupil of the WHT is re-imaged onto a lenslet array, so that sections of the aperture ~50cm in diameter are imaged separately onto the detector.  Displacements of the images from their nominal positions are proportional to the mean gradient of the wavefront over the sub-aperture.
 
 

The CCD camera records images of the spot pattern continuously at frame rates of typically 100Hz for a few tens of seconds, so that the temporal development of the wavefront distortion can be analysed. For each frame, centroids are calculated for each spot, to yield the mean wavefront tilt over the corresponding sub-aperture in the telescope pupil. The instantaneous phase aberration, as a function of position in the telescope aperture plane, can then be approximated via a fit to this set of local phase gradients.

The JOSE data can be analysed to determine whether the wavefront phase distortions follow the Tatarski scaling law, and to yield values for Fried's parameter r₀ where appropriate. The strength of the aberrations on a range of spatial scales can be conveniently studied by expressing the phase distortion as a weighted sum of the classical Zernike aberration functions. The two first-order Zernike modes represent global tilts of the wavefront over the whole telescope pupil (which result only in translations of the image at the telescope focus).  Higher order modes describe other familiar aberrations of greater spatial complexity, including defocus, astigmatism and coma.  The Zernike mode decomposition of the wavefront perturbation is found by a least-squares fit of the Zernike gradients to the measured set of subaperture phase gradients.

Noll (1976)  has calculated the expected variances of the Zernike mode coefficients for the Tatarski phase structure function.  For this model, low order Zernike terms carry more phase variance than higher orders, and the variances are proportional to r₀^-5/3. By comparing the measured variances to their theoretical values we can assess the validity of the 5/3 scaling and estimate a value for r0 by a least-squares fit.

The following figure  demonstrates this analysis for two example JOSE data sets. The measured mode variances are plotted with their theoretical values for the best-fit  value. Clearly good fits are obtained in these cases, and the distribution of mode variances is very close to that predicted by Noll.  This is true for the majority of the JOSE data set, so that Fried's parameter has a well defined value in most cases. Uncertainties for r0 are given by the standard error of the least-squares fit, and are typically +/- 5%

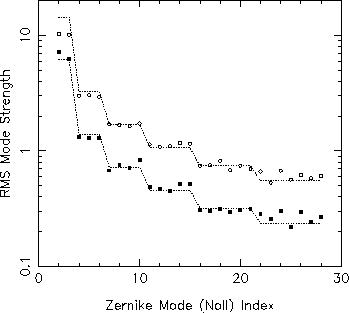
Examples of the JOSE seeing analysis. Measured rms Zernike mode  strengths are plotted with their theoretical (Noll) values for the best-fit r₀. The two examples are representative of very good seeing (solid squares,  r₀ = 30cm ) and moderate seeing (open circles, r₀ = 10cm ). Theoretical values are indicated by continuous dotted lines between the discrete modal values. Although the values for Zernike tilts (Noll orders 2 and 3) are included on the plot, they were excluded  from the least-squares fit for r₀.

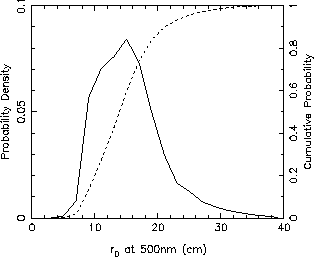
Statistics of JOSE r₀ measurements (corrected for zenith angle) are shown below. The median value (14.8cm) is very close to that obtained with the DIMM (14.9cm),   although the DIMM distribution is slightly broader than for the JOSE data. This difference results partly from year-to-year variations, since the majority of the DIMM data set was obtained in the period from October 1994 to October 1996, whereas the bulk of the JOSE observations were made in 1997 and 1998. The DIMM histogram is also derived from a larger data sample in total than the JOSE version.

References

• Noll, R.J., 1976, J.Opt.Soc.Am., 66, 207.
• StJacques, D., Cox., G.C., Baldwin, J.E., Mackay, C.D., Waldram, E.M., Wilson, R.W., 1997, MNRAS, 290, 66 (postscript).
• StJacques, D., 1998, PhD thesis, Cambridge University (postscript).

Wilson, R.W., 1998, New Astronomy Reviews, 42, 465 (postscript)