


Next: Nuggets and wrinkles
Up: Noise and statistics in
Previous: Photon noise calculation
A normalized Stokes parameter (P 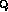 etc) is `the difference
between 2 intensity values, divided by their sum' and, since this
quotient comprises parameters which are not statistically independent,
repeated measurements do not yield a Gaussian distribution. The
non-normality becomes apparent at small numbers of detected photons, a
situation one might easily encounter in CCD polarimetry. Other
non-Gaussian distributions are sent to plague us, notably those of
degree of polarization and polarization angle in situations of low
signal to noise. Clarke and Stewart (reference in Appendix I) treat
these questions in detail; careful interpretation of data is
especially required in low signal-to-noise situations. Whether full
statistical treatment is required as a result of non-normality can be
judged from the following rules of thumb:
etc) is `the difference
between 2 intensity values, divided by their sum' and, since this
quotient comprises parameters which are not statistically independent,
repeated measurements do not yield a Gaussian distribution. The
non-normality becomes apparent at small numbers of detected photons, a
situation one might easily encounter in CCD polarimetry. Other
non-Gaussian distributions are sent to plague us, notably those of
degree of polarization and polarization angle in situations of low
signal to noise. Clarke and Stewart (reference in Appendix I) treat
these questions in detail; careful interpretation of data is
especially required in low signal-to-noise situations. Whether full
statistical treatment is required as a result of non-normality can be
judged from the following rules of thumb:
-
When the number of detected photons per elementary detector (i.e.
after on-chip binning, but before software binning) is less than about
1000, the distribution of the normalized Stokes parameters is
noticeably skew and this must be allowed for in proper binning or
averaging procedures.
-
Degree of polarization is always positive. When P is less than
about 5 times the standard error of the normalized Stokes parameters,
straightforward averaging of P produces biased results.
-
Confidence intervals, for estimates of P from a sample of
observations, are asymmetric in the domain P/
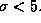
-
Although the determined values of polarization angle are unbiased,
their symmetric distribution about the mean is kurtose and confidence
intervals do not correspond to those for a normal distribution.
Attention to this detail is only warranted in the domain
P/
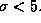
-
When
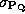 is not equal to
is not equal to
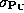 (as may be the case when the ISIS standard recipe
is used under conditions of varying extinction or pressure of time
near sunrise),
(as may be the case when the ISIS standard recipe
is used under conditions of varying extinction or pressure of time
near sunrise), 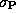 and confidence intervals of degree
and angle of polarization will depend on the relative values of
and confidence intervals of degree
and angle of polarization will depend on the relative values of
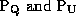 (in other words on what the polarization angle
happens to be).
(in other words on what the polarization angle
happens to be). -
A prescription for a (statistically) maximally effective observing
campaign is given by Clarke and Stewart in their last section;
however, add your own considerations of what fraction of time to spend
on calibration of zeropoint, angle and degree of polarization.



Next: Nuggets and wrinkles
Up: Noise and statistics in
Previous: Photon noise calculation
manuals store
Tue Oct 7 17:34:45 BST 1997
![]() etc) is `the difference
between 2 intensity values, divided by their sum' and, since this
quotient comprises parameters which are not statistically independent,
repeated measurements do not yield a Gaussian distribution. The
non-normality becomes apparent at small numbers of detected photons, a
situation one might easily encounter in CCD polarimetry. Other
non-Gaussian distributions are sent to plague us, notably those of
degree of polarization and polarization angle in situations of low
signal to noise. Clarke and Stewart (reference in Appendix I) treat
these questions in detail; careful interpretation of data is
especially required in low signal-to-noise situations. Whether full
statistical treatment is required as a result of non-normality can be
judged from the following rules of thumb:
etc) is `the difference
between 2 intensity values, divided by their sum' and, since this
quotient comprises parameters which are not statistically independent,
repeated measurements do not yield a Gaussian distribution. The
non-normality becomes apparent at small numbers of detected photons, a
situation one might easily encounter in CCD polarimetry. Other
non-Gaussian distributions are sent to plague us, notably those of
degree of polarization and polarization angle in situations of low
signal to noise. Clarke and Stewart (reference in Appendix I) treat
these questions in detail; careful interpretation of data is
especially required in low signal-to-noise situations. Whether full
statistical treatment is required as a result of non-normality can be
judged from the following rules of thumb: