For faint objects sky polarization must be corrected for. Sky polarization can reach very high values compared to that of astronomical objects, so sky correction becomes important at brighter magnitudes than one may be used to from photometry.
The desired quantity is P ![]() (and P
(and P ![]() ),
the true degree of polarization of the light of the object.
We express this in terms of the observables.
),
the true degree of polarization of the light of the object.
We express this in terms of the observables.
![]()
![]()
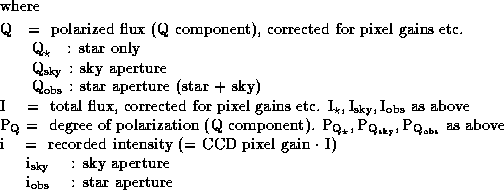
Equation A is exact, while B contains 2 implicit approximations:
For a great deal of work, B will suffice. It does not require any flat-fielding, the spectra from the star and sky apertures can be reduced in the same way, with a final small correction depending only on the recorded intensities of star and sky spectra. Furthermore, for bright stars and/or dark sky, the entire correction is negligible.
When approximation B is not good enough (this is a question of
scientific requirements), one uses A and will need to know true
(but relative) star and sky fluxes, ![]() and
and ![]() .
For this one needs (relative) sensitivities (i.e. ``system gain''
including such things as grating used, its wavelength setting, any
vignetting in the optical system) for the pixels recording the spectra
(o and e-ray separately) from star and sky apertures. The best way to
obtain these is to expose an unpolarized flat field through the
polarimetric system. The best flat field is blue sky (necessarily with
an ND filter, which may somewhat compromise the flatness; a filter far
from the focal plane is best). To depolarize this flat field, use the
halfwave plate in a continuously rotating mode, making sure there are
many cycles within the exposure time. To transfer a blue-sky flat
field to night-time observations, one could use a tungsten lamp (which
probably does not produce a very flat field, since the specification
was very slack), relying on constancy of the pattern of
illumination by the lamp. Note that choice and setting of the grating
- and any auxiliary anti-scattering filters - should be the same for
programme and flat-field exposures. If one trusts CCD constancy more
than constancy of the lamp illumination pattern, the lamp exposures
are omitted.
.
For this one needs (relative) sensitivities (i.e. ``system gain''
including such things as grating used, its wavelength setting, any
vignetting in the optical system) for the pixels recording the spectra
(o and e-ray separately) from star and sky apertures. The best way to
obtain these is to expose an unpolarized flat field through the
polarimetric system. The best flat field is blue sky (necessarily with
an ND filter, which may somewhat compromise the flatness; a filter far
from the focal plane is best). To depolarize this flat field, use the
halfwave plate in a continuously rotating mode, making sure there are
many cycles within the exposure time. To transfer a blue-sky flat
field to night-time observations, one could use a tungsten lamp (which
probably does not produce a very flat field, since the specification
was very slack), relying on constancy of the pattern of
illumination by the lamp. Note that choice and setting of the grating
- and any auxiliary anti-scattering filters - should be the same for
programme and flat-field exposures. If one trusts CCD constancy more
than constancy of the lamp illumination pattern, the lamp exposures
are omitted.
[ TIFF ]
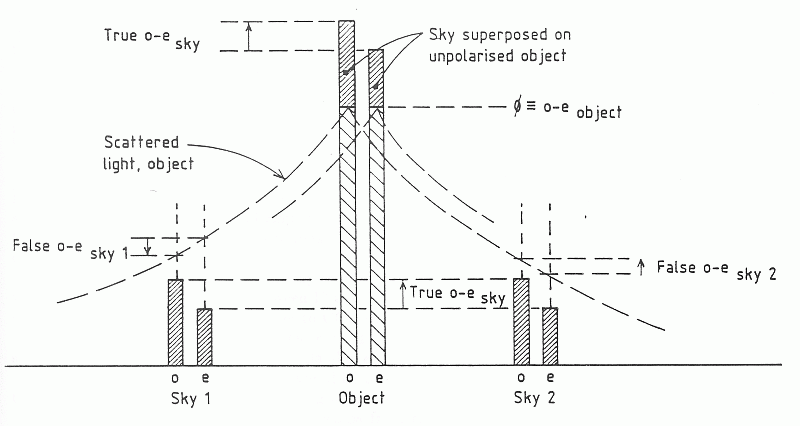
Figure 6: Scattered light causing false sky polarization. See text.
Note that the sky region may be affected by scattered light from your object (Fig 6). One could take a second set of frames exposed on nearby clear sky to avoid confusion with scattered light from the object. Processing similar to that for the object spectra will yield the degree of polarization for the sky signal. Alternatively, one could take the sky regions symmetrically on either side of the object. This to first order eliminates the influence of scattered light from the determination of sky polarized flux; the total sky flux also contains a scattered component, to be removed in some other way (such as scattered-light modeling). For more detail on problems of scattered light, see Section 3.5.
To check on whatever method of sky subtraction one uses, take a few
sky frames exactly as one takes star frames. Use the ``stellar''
spectrum in these frames to correct for sky in the observations
proper.
NB. There seems to be no way to determine how the extinction
varied between the 2 frames, one just waits for seemingly photometric
conditions and keeps one's fingers crossed.
When only one sky aperture is available, a good approach to reducing errors is to take a second complete set of exposures, this time with the star in the ``sky'' aperture. As long as the errors involved are small, they should largely cancel in the average of the 2 sets.