Utilising the filter in uncollimated (i.e. convergent or divergent) light involves slightly more complex considerations. Here, light enters the filter at a range of angles, so that different rays undergo unequal wavelength shifts. This results in not only a central wavelength shift, but a broadening of the bandwidth and lower peak transmission.
As a rough approximation, relatively uniform beams (with full cone angles
less than 20
) will undergo peak shifts of aproximately one half of
that which would be predicted for a collimated beam at the maximum angle
of incidence of the cone.
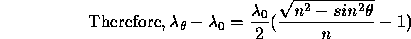
The filters were specified for a focal ratio of 4.5, having a maximum angle
of incidence of the cone of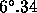 
, and a refractive index of the dielectric stack of 2.1.
Substituting these values in the equation,
lambda_theta - lambda_0 = -0.00069lambda_0
The focal ratio of the INT prime focus is 3.29, which gives a maximum angle
of incidence of the cone of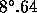 
, so, substituting again into
the equation,
Therefore, at the INT prime focus, the central wavelength (i.e. the wavelength
of peak transmission) is shifted towards shorter wavelengths by 0.06% from
the specified central wavelengths, or 0.13% from the
measured central wavelength in a collimated beam.
For example, for an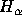 
filter
with specified central wavelength 6558Å, the effective central wavelength
will be 6549.6Å.
Similarly for the WHT prime focus the maximum cone angle is
,
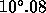and the central wavelength is shifted towards shorter wavelengths by
0.10% from the specified central wavelength, or 0.17% from the measured
central wavelength in a collimated beam.