[ TIFF ]
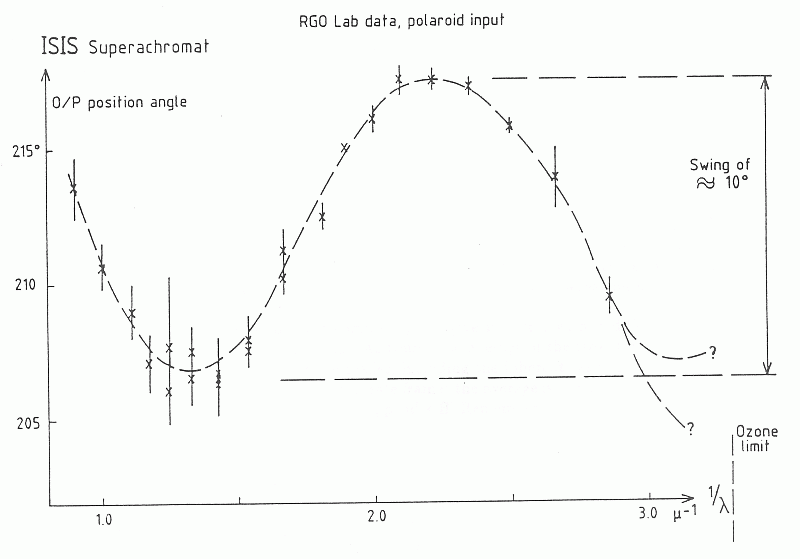
Figure 9: Wavelength-dependence of the apparent polarization angle. This is a direct consequence of specifying super-achromatism of the retardation; observations need to be corrected for this effect.
The effect of the halfwave plate on the polarization angle of the beam is a function of wavelength. This causes the instrumental frame for measuring the direction of polarization to exhibit dispersion. The necessary correction can again be obtained by measuring any star through the 100 % polarizer. The polarization angle obtained from such a polarized source should be independent of wavelength and any deviation from that situation is due to the halfwave plate. The inverse should be applied as a correction to the other observations; you may choose any wavelength as your reference at this point. Fig. 9 shows laboratory data of the ISIS halfwave, Fig. 12 a sample observation.

[ TIFF ]
Figure 9: Wavelength-dependence of the apparent polarization angle.
This is a direct consequence of specifying super-achromatism of the
retardation; observations need to be corrected for this effect.
At this point, the data are defined relative to some instrumental reference frame (which may have changed since you last used the ISIS system; too many steps are involved, both hardware and software, to make an attempt at fixing the system once for all). You must therefore measure the polarization of at least one polarization standard star to calibrate the instrumental zero-angle (also useful for verifying degree-of-polarization scale and reduction procedures). References to appropriate standard stars are given in Appendix H; see Bastien et al. for a recent report on variability of `standards'.
To determine the polarization angle from scratch, several methods are available, not all equally convenient. One good possibility is to observe a low-albedo asteroid at a phase angle which yields appreciable polarization. For the polarization to have reasonable values, the phase angle of the asteroid needs to be in the range 10 to 20 degrees, or above 30 degrees. In the former case, the polarization vibration will be parallel to the Sun-Asteroid-Earth plane and in the latter case it will be normal to this scattering plane. Preparations for such observations must be done beforehand, so that the coordinates and the phase angle of the asteroid are known; careful tracking will be required.
Another promising method is to observe blue sky in the zenith (or close to the zenith at anti-solar azimuth if the zenith itself cannot be reached). By symmetry (but: waves on the sea, structure in cirrus clouds, how perfect is the symmetry?), any remaining linear polarization in the multiple scattering should on La Palma closely average out to zero, while the polarization angle of the singly-scattered component is determined by the Sun's azimuth. This method needs to be verified, but could be very convenient; together with flat fields, it could in future make up the afternoon run of the seasoned observer.
An old and tried method is due to Gehrels and Teska and is also described in Serkowski (p. 411); it involves reversing a Polaroid suspended in front of a horizontal telescope. Bring your own Polaroid and enquire in good time what it takes to make WHT observe horizontally. An alternative `mechanical' method is described in Dolan & Tapia (see Appendix H on standard stars); for this method to be used operationally, the exact orientation of the polarization of the analyser beams will have to be determined with respect to the slit, after which drift of a star along the slit can be used for routine verification.