




Previous: Principles of operation (cross--dispersed mode)
Up: Principles of operation (cross--dispersed mode)
Next: Central wavelength and order number
Previous Page: Principles of operation (cross--dispersed mode)
Next Page: Central wavelength and order number

A choice of two gratings is provided with UES, one with 31.6
lines/mm and one with 79.0 lines/mm. It is important to realise
that the choice of grating is not determined by the spectral
resolution required, as in a conventional first order spectrograph
such as ISIS. Instead, the choice of grating is determined
by a trade-off between wavelength coverage and the quality of
sky subtraction.
In order to see why this is the case, its worth briefly restating
the basic equations governing diffraction by a grating. The grating
equation describes the condition for constructive interference:


The angular dispersion is obtained by differentiating this:

The dispersion is a function only of the angles at which the grating
is used, and not a function of the groove spacing.
The two UES gratings have nearly the same blaze angle
(64.95 degrees for the 31.6 echelle and 63.96 degrees for the 79.0 echelle),
and hence are
used with similar values of i and 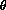 . This means
that at a given wavelength they provide almost identical spectral resolution
as can be seen from Tabs. 15 and 16.
. This means
that at a given wavelength they provide almost identical spectral resolution
as can be seen from Tabs. 15 and 16.
The difference between the two gratings is that, at any given
wavelength, the grating equation implies they must be operated
at a different interference order.
For example, observations at 5000Å would use either the 31.6
lines/mm grating in order m 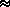 114, or the 79.0 lines/mm
grating in order m
114, or the 79.0 lines/mm
grating in order m 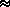 45 (see Tabs. 15
and 16 ). The principal
effect of this is that the wavelength range of each order, normally
referred to as the Free Spectral Range (FSR) is different.
The FSR is given by:
45 (see Tabs. 15
and 16 ). The principal
effect of this is that the wavelength range of each order, normally
referred to as the Free Spectral Range (FSR) is different.
The FSR is given by:

At any given wavelength, the 79.0 lines/mm grating will have
2.5 times the free spectral range of the 31.6 lines/mm
grating; the orders are 2.5 times longer, and hence 2.5 times
further apart. Since the dispersion is the same, this means that
for a fixed detector size, the 79.0 lines/mm grating provides
less wavelength coverage, but more space between the orders
to measure the sky background.
When deciding which echelle to use, it is therefore necessary
to consider how long a slit you need to get adequate sky subtraction,
and how many exposures will be required to cover the required
wavelength range.
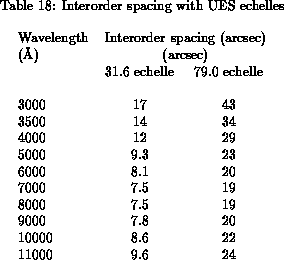
The inter-order spacing with both echelles
at various wavelengths is summarised in Tab. 18.
This assumes no focal modifier lenses are in the beam.
The slitlength used should be slightly shorter than this
inter-order spacing, in order to leave a gap between the orders.


It is possible to estimate the number
of exposures required to cover a given wavelength range using
the data in
Tabs. 15 and 16. These tables
give the length and separation on the detector of each
order.
This calculation can be carried out much more easily using
graphical means, and the ECHWIND programme has been developed
for this purpose.
ECHWIND draws a complete echellogram on an image display,
together with a box representing the size and shape of the detector
in use. The position of individual spectral lines can also
be marked on the display. The user can then move the detector
window around using the mouse. At each position, the screen displays
the minimum and maximum wavelengths and order numbers falling on the
detector. The position of the detector window can be marked on the
screen so as to ease preparation of observations where multiple
overlapping wavelength ranges are required.
The output of the programme is the central wavelength
and order number of each exposure.





Previous: Principles of operation (cross--dispersed mode)
Up: Principles of operation (cross--dispersed mode)
Next: Central wavelength and order number
Previous Page: Principles of operation (cross--dispersed mode)
Next Page: Central wavelength and order number









 . This means
that at a given wavelength they provide almost identical spectral resolution
as can be seen from Tabs.
. This means
that at a given wavelength they provide almost identical spectral resolution
as can be seen from Tabs. 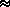 114, or the 79.0 lines/mm
grating in order m
114, or the 79.0 lines/mm
grating in order m 
