



Previous: CCD systems on the INT
Up: CCD Detectors
Previous Page: Cosmic ray events
Next Page: Atmospheric extinction





Previous: CCD systems on the INT
Up: CCD Detectors
Previous Page: Cosmic ray events
Next Page: Atmospheric extinction
Once the signal to noise ratio required for the observation to be successful has been defined, you want to estimate the integration time needed to achieve it. Here we outline how to perform this calculation.
The noise level for a typical astronomical observation will consist of three
components. The first component is signal independent noise arising from the
detector itself (readout noise). Secondly, we have shot noise in the signal
from the object being observed. This follows a Poisson distribution, so its
variance is equal to the signal level. Finally, we also have shot noise in any
background signal (particularly the sky background and preflash). Adding the
noise terms in quadrature, the signal to noise ratio (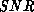 ) is given by:
) is given by:
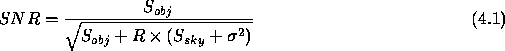
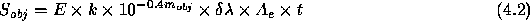
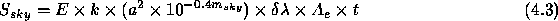
=Total signal from object being observed *
=Signal per pixel from sky background * R=Number of pixels in seeing disk *
=RMS readout noise in electrons per pixel * E=Responsive quantum efficiency of the CCD * k=number of photons s
A
cm
at the bottom of the atmosphere from * a star of magnitude
. At 548 nm k
1000 photons s
A
cm
*
=apparent magnitude of the object being observed *
=sky brightness in magnitudes per arcsec
(see section 1.3.2) *
=pixel area in arcsec
*
=effective filter bandwidth in Å *
=effective aperture of telescope, or geometrical collecting area
efficiency * t=exposure time in seconds
The signal to noise ratio obtained therefore depends on both the efficiency of the detector and the level of detector noise.
Table 2.2 gives estimates of the efficiency of the GEC CCD at a number of wavelengths from Figure 2.1.

The detector noise of a CCD is dominated by the readout noise, which is 5-10 electrons per pixel for the coated GEC P8603 (Table 2.1). Note however that the number we really need is the readout noise per resolution element, not the readout noise per pixel. The readout noise per resolution element depends on two factors:
A first relatively straightforward but important case is where the noise level is dominated by shot noise on the sky background (sky limited observations). This is usually the case for low resolution spectroscopy or imaging observations. Typical values for the sky brightness on La Palma in a variety of wavebands are given in the Observer's Guide. As far as signal to noise is concerned, the most effective detector for sky limited observations is simply the most efficient.
We now consider the case where the sky background can be neglected, normally the case for high resolution spectroscopy or bright objects. As we noted above, observations at high signal levels, where we might expect a high signal to noise ratio, will be best suited for the CCD, whereas observations at low signal levels, and low signal to noise ratio, will be best suited for the IPCS. The basic message here is that if you intend to take short exposures of fairly bright objects, you should probably use the CCD, whereas if you expect to observe the same object all night to obtain adequate signal to noise ratio (S/N < 30), you should probably be using the IPCS.
As discussed above, the signal to noise ratio obtained from an observation depends on two factors: the level of detector noise, and the number of photons detected in each resolution element. In what follows we present the data necessary to estimate the number of photons incident on the detector in each resolution element.
For a system with no light losses, it is straightforward to show that the number of photons incident in each resolution element is given by:
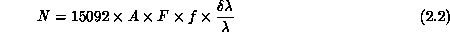
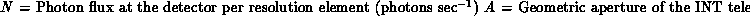
Unfortunately, only a small fraction of these photons are actually detected, perhaps 1 per cent! This low efficiency is due to a number of factors, discussed in what follows.